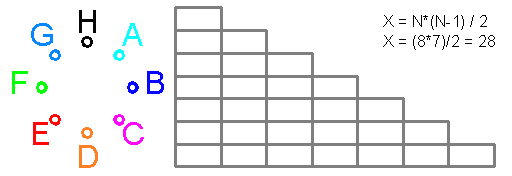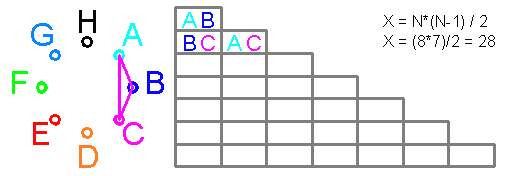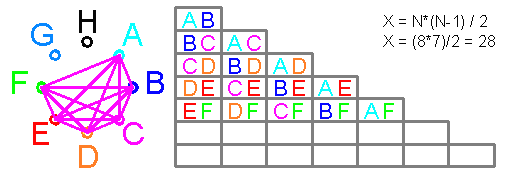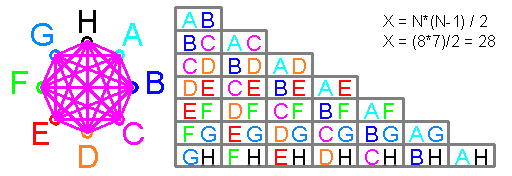
Квадрат Экономии Данилиных QED
Ошибки должны быть дешёвыми и для удешевления
проигрышей создан Квадрат Экономии Данилиных QED
заодно олицетворяющий актив и пассив ведь незачем
участвовать крупными суммами в возможных проигрышах.
Применяя Квадрат Экономии Данилиных QED происходит
ожидание выигрыша без крупных проигрышей и в итоге
получается дождаться событий с коэффициентом 100.
Квадрат Экономии Данилиных QED заполненный ставками
соблюдая правила ставок экономит затраты в десятки раз.
Квадрат Экономии Данилиных QED исключая азарт
олицетворяет догон многопоточный догон многоканальный.
Квадрат Экономии Данилиных
вариант ускоряющийся где за каждое
развитие выше вероятность выиграть
 
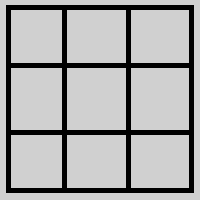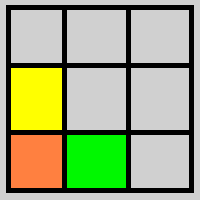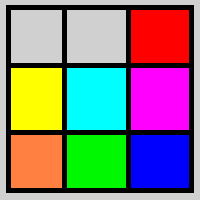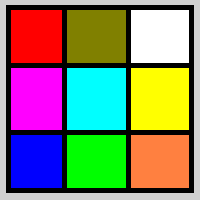
Ставки развиваются по горизонтали равными ставками
и по вертикали повышением ставок до уровня выше
и вновь переходят в ставки по горизонтали причём выигрыш
в любой точке поглощает в столбце все проигрыши ниже.
Квадрат Экономии Данилиных с постоянными вероятностями угадать
с постоянными множителями ставок при выигрыше после проигрыша
ведут к повышению выигрышей
Квадрат Экономии Данилиных с переменными вероятностями угадать
с переменными множителями ставок при выигрыше после проигрыша
ведут к понижению выигрышей
Несмотря на теорию единственной ставки в 1 время
возможны 2 ставки в 1 время при условии когда и выигрыш
и проигрыш ставки приводит к следующей ставке в нижней горизонтали
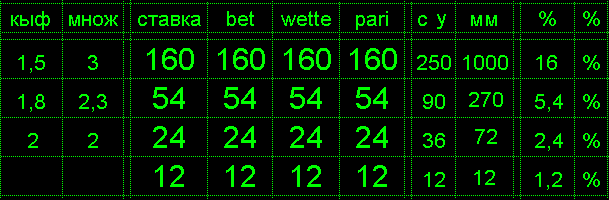
Квадрат Экономии Данилиных КЭД для ставок с любым коэффициентом
отыгрывающий все предыдущие проигрыши по вертикали с заданным выигрышем
и возможно вводить требующуюся прибыль
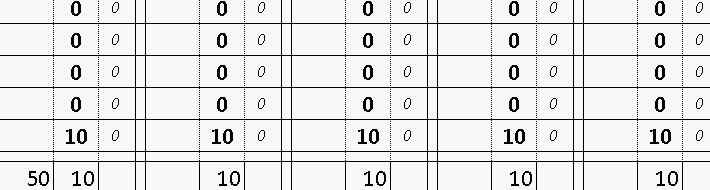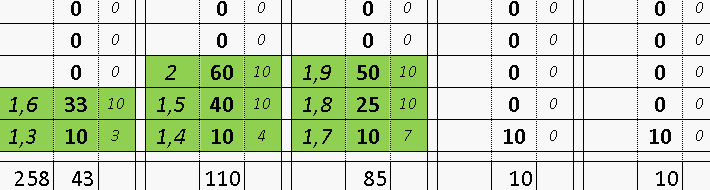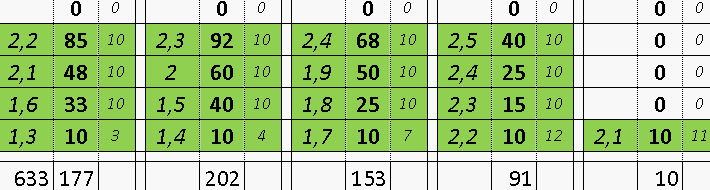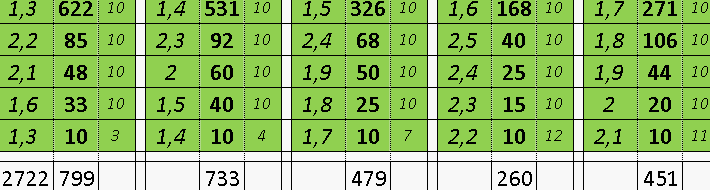
При выигрыше вертикаль обнуляется и все столбцы правее сдвигаются влево
Возможно применять свои правила например заполнять сначала горизонталь
или при выигрыше удаляя отыгранные ставки. Использованы формулы:
=ЕСЛИ(C3=0;0;(10+СУММ(D4:D$7))/(C3-1))
=ЕСЛИ(C3=0;0;C3*D3-СУММ(D3:D$7))
Применяется стратегия догон и догоняется коэффициент.
Отыграть сумму проигрышей возможно за несколько выигрышей
и выйдя в плюс лучше не отыгрывать бывшие проигрыши.
В общем виде математический финансовый менеджмент:
понижение коэффициента и повышение вероятности выигрыша
и повышая ставки по множителю зависимого от коэффициента.
При коэффициенте К множитель ставки М=1+(1/(К-1)).
При коэффициенте К=3 множитель ставки М=1+(1/(3-1))=1,5.
Для вероятности около 1/3 предел несовпадения подряд
равен Д=12 и при начальной ставке 1% на 12 ходу
ставка должна быть "1% умножить на М=1,5 в степени 12"
и получается ставка должна быть 130% баланса.
От коэффициента зависит множитель повышения следующей ставки.
От вероятности зависит число ставок до проигрыша баланса.
Математические законы справедливы во всех лотереях и
важно знать дюжину пределов несовпадения подряд наизусть.
Умножение постоянных вероятностей C+р^N=1
олицетворяет вероятность вероятности и создаёт формулу
N = LOG(1-C)/LOG(1-p)
С - вероятность выигрыша гарантированного
р - вероятность выигрыша события.
Например задача: число несовпадений подряд
с вероятностью 99% для вероятности 48,65%
N = LOG(1-0,99)/LOG(1-0,4865) = 7
и значит на вероятности около 50%
легко неугадать 7 раз подряд
Упрощённо возможно рассчитывать по формуле N = 7+(5*(1/x-2))
например х=0,1 N= 47 нормально и х=0,78 N= 4 нормально.
Те же формулы справедливы и для вероятностей выше 50%.
Геометрические прогрессии содержащие в условии или в решении
смысл "в какую степень надо возвести" решаются через логарифм.
Используя предел несовпадения подряд в таблицах
обнаруживается волна или период угадываний 2-х видов:
1-й вид: волна или период - как сама вероятность
через количество тиражей и там где вероятность 1/3
там волна или период угадывания через 3 тиража;
2-й вид: волна или период - как предел несовпадений подряд
и там где вероятность 1/3 там волна или период угадывания
через 12 тиражей и возможно несколько ставок при сигнале.
Есть эмуляторы показывающие как динамично развивается
Квадрат Экономии Данилиных QED и при условии обнуления
значений ставок и при остановке при достижении выигрыша
Квадрат Экономии Данилиных QED показывает выигрышность
даже при применении одинаковых данных
для исследования каждой трети рулетки.
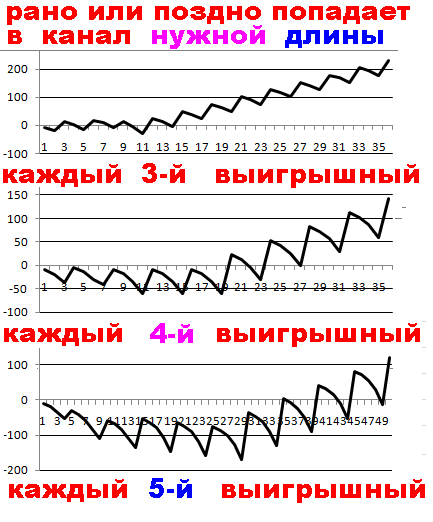
График ставок используя Квадрат Экономии Данилиных QED
выглядит как фрактал состоящий из волн составляющих
крупную волну и такой же график получается
при использовании математически обоснованных систем игры.
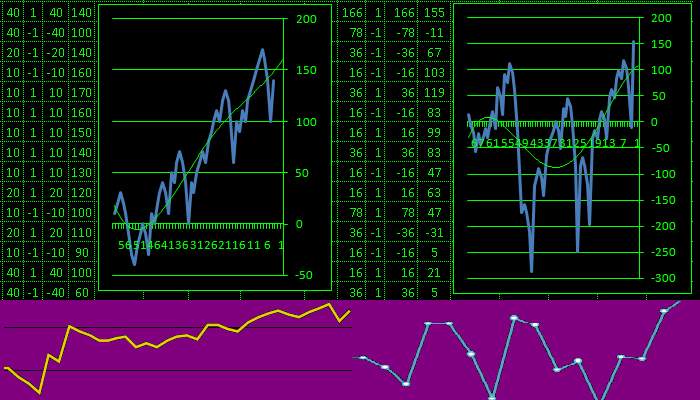
Успех
Вероятность |
1 из ...
|
|
2 |
3 |
4 |
5 |
10 |
100 |
1,5 |
1,33 |
|
1 /… |
Win 1 from…
Probability |
Отказ
Вероятность |
% |
|
50% |
67% |
75% |
80% |
90% |
99% |
33% |
25% |
|
% |
Lose %
Probability |
| |
|
|
Подобные ПОДРЯД |
|
|
|
| Надёжность |
99 % |
|
7 |
12 |
16 |
21 |
44 |
458 |
4 |
3 |
|
99 |
Reliability |
| Надёжность |
99,5 % |
|
10 |
17 |
24 |
31 |
66 |
687 |
6 |
4 |
|
99,9 |
Reliability |
| Надёжность |
50 % |
|
1 |
2 |
2 |
3 |
7 |
69 |
1 |
0 |
|
50 |
Reliability |
| |
|
|
Similar IN ROW |
|
|
|
Успех
Вероятность |
1 из ...
|
|
2 |
3 |
4 |
5 |
10 |
100 |
1,5 |
1,33 |
|
1 /… |
Win 1 from…
Probability |
Отказ
Вероятность |
% |
|
50% |
67% |
75% |
80% |
90% |
99% |
33% |
25% |
|
% |
Lose %
Probability |
Угадать вероятность 25%=1/4=0,25 и получить надёжность 99% нужно 16 подряд действий
Guessing for probability of 25%=1/4=0.25 and getting 99% reliability requires 16 actions in a row
развивается QEDbasic
и мозговой штурм ищет как распознавать иглы
и пока добавил счётчики удач и неудач
и рассчитываем деление несовпадений подряд
чтобы QEDbasic распознавалась игла меньше предыдущей
обновил QEDbasic строящий Квадрат Экономии Данилиных
создающий текстовые отчёты и возможно всё дополнять
внутри одного из отчётов анимация КЭД правильно надеюсь
особенность: считается вероятность и множитель
и далее возможны варианты ввода множителя или плюс/минус 10%
из массива считывается номер и определяется доля
от 1 по нужный номер и для других вариантов возможно менять
исходные данные со смещением или пересоздать массив номеров
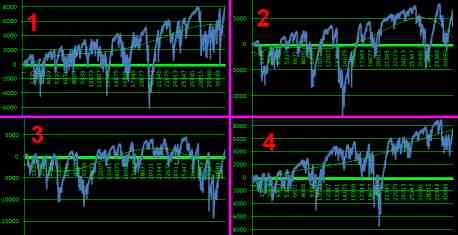
видим характерные виды графиков с углами и важнее волны
на графиках тестируемый массив на вероятностях 1: 2 3 4 1,5 1,33
и как видим проблема во временной неспособности эмулятора КЭД
распознавать иглу приводящую к обнулению КЭД лишь при максимуме
зато в прямом эфире человек может обнулять Квадрат Экономии Данилиных
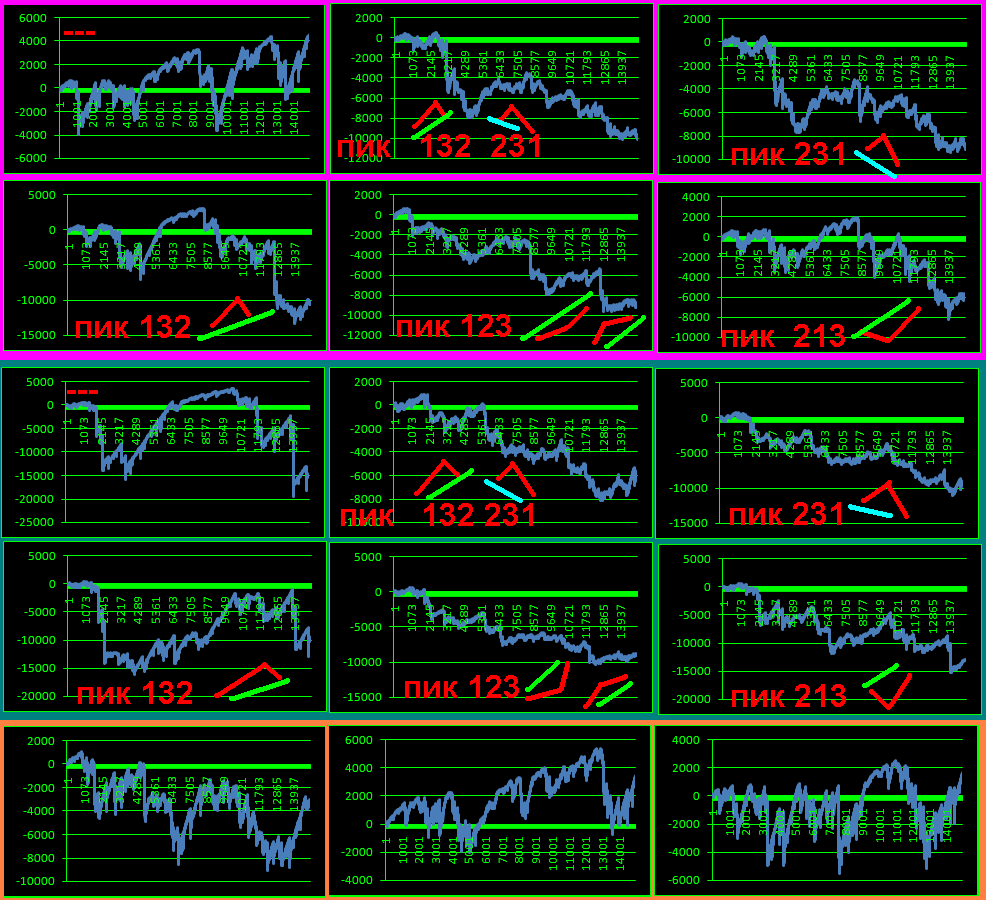
обновил QEDbasic исследуя иглы
проще оказалось реализовать разделение по 100 тиражей
и в каждом отрезке смотреть 6 ситуаций из них 4 перспективных
и в принципе по схемам около букв на картинке ясно
мелкие отрезки оказались хуже и некоторые иглы и все иглы
тащили график вниз при любых номерах
дальше ещё исследую на разных вероятностях
и научусь применять деление несовпадений подряд
а пока перспективным оказался вид игла132:
баланс: наименьший / наибольший / средний
как понижение баланса когда локальная игла
обнуление только вертикали КЭД
при игла132: мало-много-средне
показывает перспективность исследований
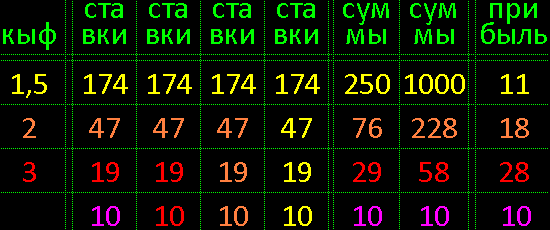
в данном случае кыф 2 для 18/37 номеров
1. массив номеров заготовленный
2. массив номеров перевёрнутый
3. и 4. массивы номеров случайные
и далее исследую на других вероятностях
но каждый вариант вызывает дерево вариантов
применяя КЭД для участия в рулетке с частыми тиражами
думаю удобно изготовить ячейки КЭД из бумаги
с числами с соответствующими ставками
и раскладывать на столе добавляя и убирая ячейки
игла132 подсказывает: старт и следим максимум и
чуть сложился игла132 буквально: половина между
началом и максимумом тогда обнулять столбец КЭД
означающий выиграла игла и дальше мало ставить
подтверждение моей теории
когда есть фаворит нечет чаще
из-за отсутствия доли чётных ничьих
особенно применив Квадрат Экономии Данилиных
Квадрат Экономии Данилиных содержит
точек проигрыша Х и точек выигрыша X^2-X
из чего возможно в будущем посчитать коэффициент
отдачи и возврат вложений для каждого
варианта КЭД в зависимости от стороны КЭД
начальные минимальные ставки
возможны на любой коэффициент
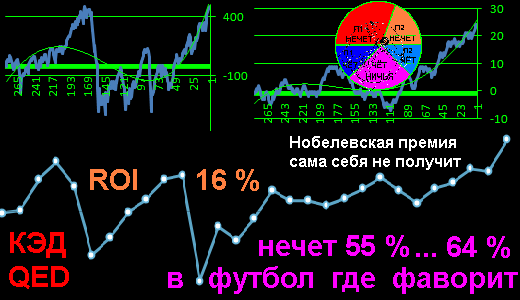
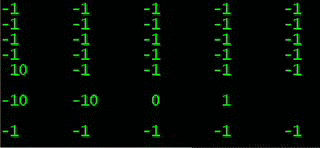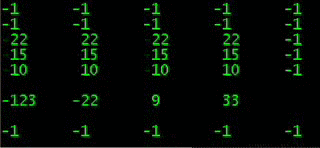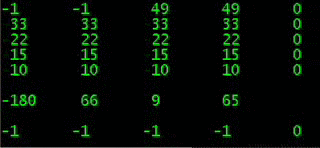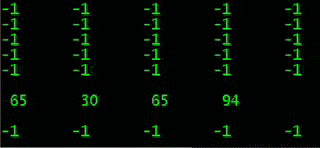
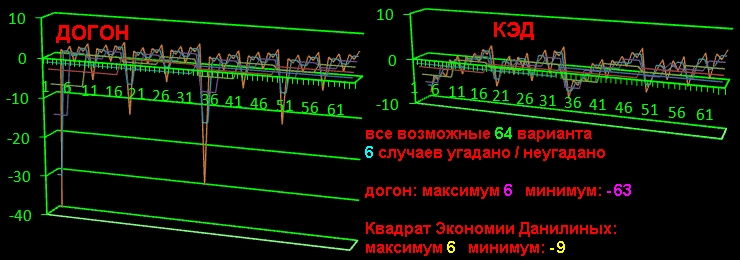
графическое изображение выгодности КЭД:
все возможные 64 варианта 6 случаев угадано / неугадано
догон: максимум: 6 & минимум: -63
Квадрат Экономии Данилиных: максимум 6 & минимум: -9
Инь и Ян вероятности исследует:
? выиграли повышая вероятность угадать ?
сначала вероятность угадать 1/6
далее вероятность угадать 1/4
далее вероятность угадать 1/3
далее вероятность угадать 1/2
далее вероятность угадать 2/3
далее вероятность угадать 3/4
далее вероятность угадать 5/6
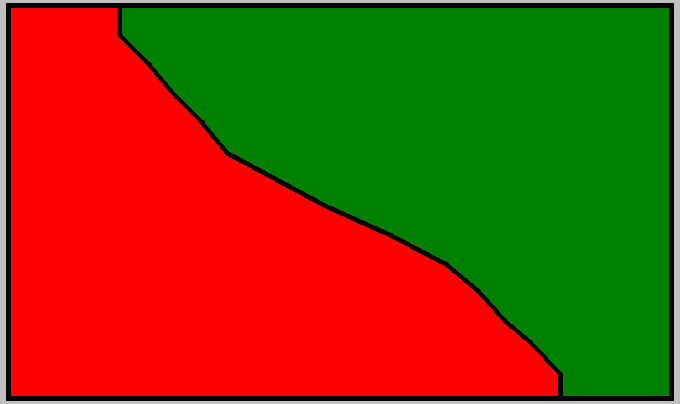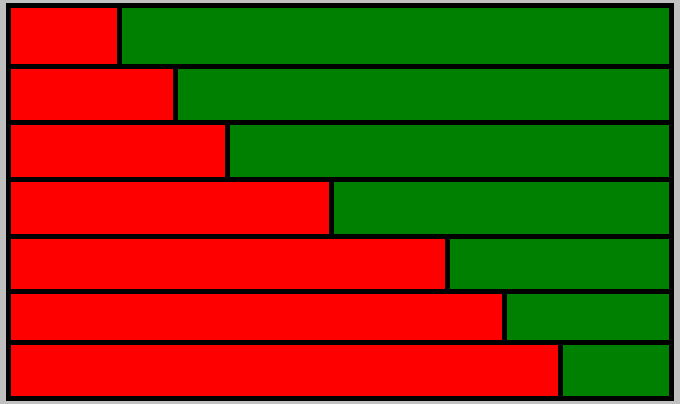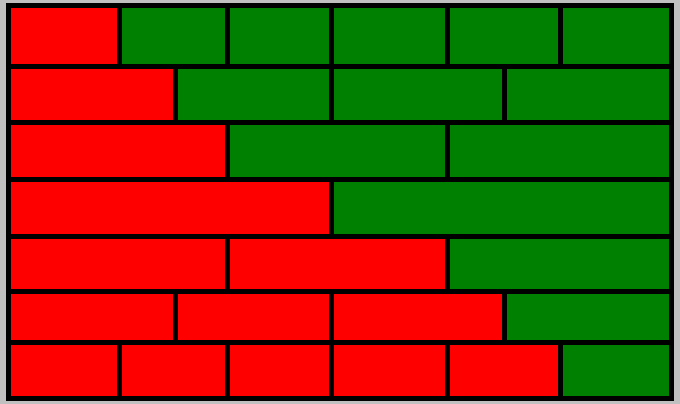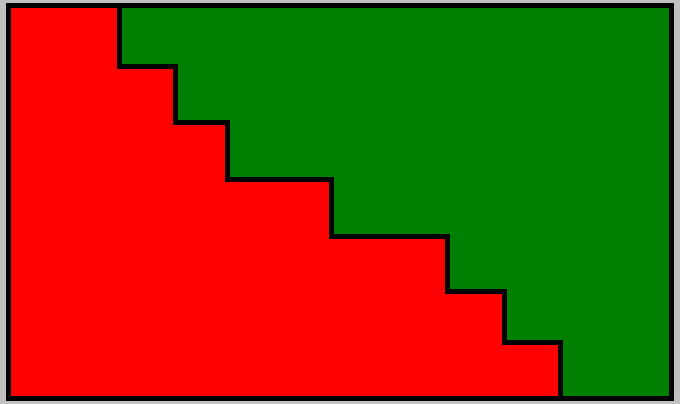
возможный Квадрат Экономии Данилиных и рулетка
долгожданный график сумм затрат:
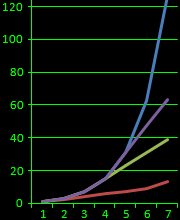 |
простой догон самый затратный
разные уровни КЭД гораздо экономичнее
треугольники между графиками и есть экономия
ведь в выражении Квадрат Экономии Данилиных
главное слово Экономии
и Квадрат главное и Данилиных тоже главное
все слова главные
|
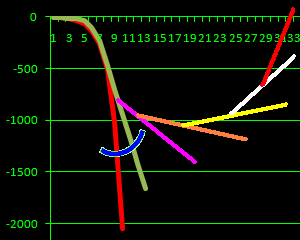 |
математический форум обсуждая проверку последовательности
случайной на случайность показал: там математики только копируют
чужую демагогию из старых книг и даже не способны задуматься
над распределением повторений событий подряд
неудивительно: в учебниках теории вероятностей искомые формулы
случайно отсутствуют но могли бы смоделировать в excel
на примере вероятности 50% сколько раз было 7 раз подряд
и другие количества признаков подряд
чтоб соответствовали формулам включающим логарифм
иначе генератор случайных чисел ... фальшивый
Исследуя логарифм получается:
формула включающая логарифм вытекает из расчёта
вероятности угадать подряд события равновероятные
Например простейшее: 0,7*0,7*0,7 = 0,7^3 = 0,343
в какую степень надо возвести 0,7 чтобы получить 0,343
и в 20-м веке формулу восстановил Андрей Данилин
N = LOG(0,343)/LOG(0,7) = 3
и соответствующая формула для неугадывания
Умножение постоянных вероятностей C+р^N=1
и в 20-м веке формулу восстановил Андрей Данилин
N = LOG(1-C)/LOG(1-p)
С - вероятность выигрыша гарантированного
р - вероятность выигрыша события.
Например задача: число несовпадений подряд
с вероятностью 99% для вероятности 48,65%
и в 20-м веке формулу восстановил Андрей Данилин
N = LOG(1-0,99)/LOG(1-0,4865) = 7
и значит на вероятности около 50%
легко неугадать 7 раз подряд
Упрощённо можно рассчитывать:
формулу открыл Андрей Данилин
N = 7+(5*(1/x-2))
например х=0,1 N=47 нормально и х=0,78 N=4 нормально.
Те же формулы справедливы и для вероятностей выше 50%.
Фальсификация случайности
Исследуя возможность фальсификации случайных
за час были созданы программы qbasic qb64
и таблица использующая формулы
=СЛУЧМЕЖДУ(0;1)
=ЕСЛИ(B3=B2;C2+1;0)
=СЧЁТЕСЛИ(C$3:C$55000;D2)
=СУММ(E2:E10)
=E2/E3
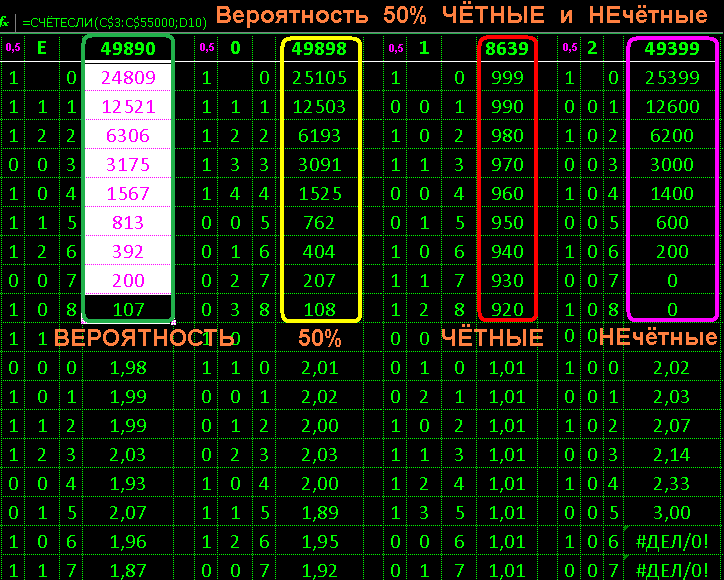
идея: фальсифицировать вероятность 50%
результаты:
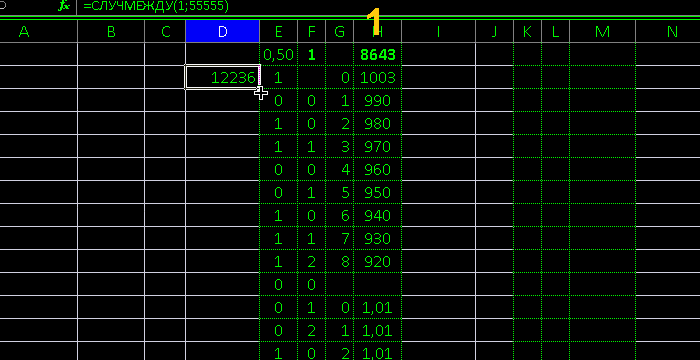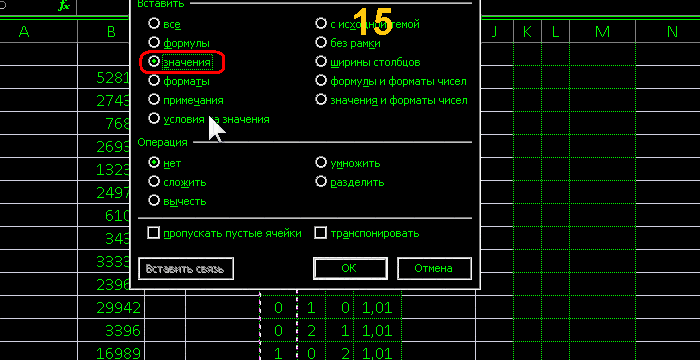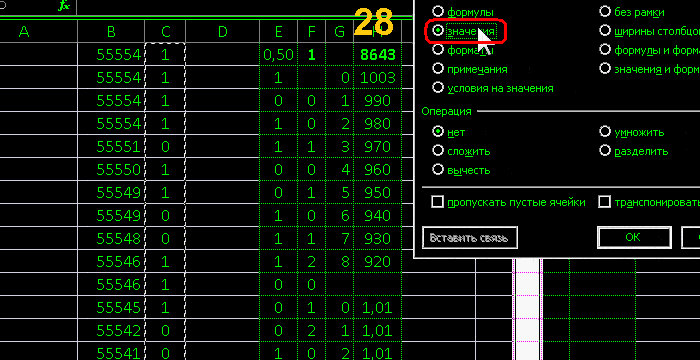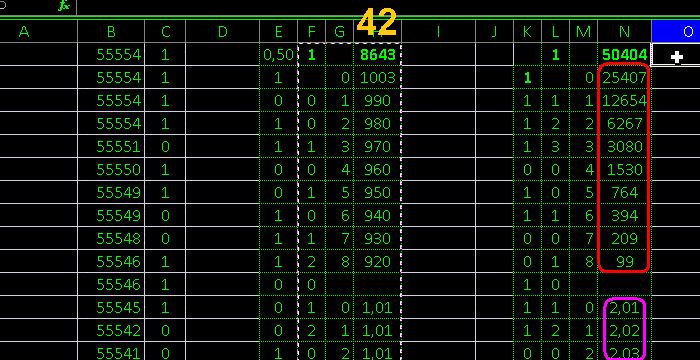
исследование E зелёным чисто excel:
случайные распределились закономерно
исследование 0 жёлтым qb 0:
случайные распределились закономерно
исследование 1 красным qb 1:
явная подделка равное число подряд
исследование 2 лиловым qb 2:
умная подделка но не запрограммированы все возможные
и виден перекос из-за алгоритма
вывод: определить фальшивые случайные реально
' 0.bas
OPEN "0.txt" FOR OUTPUT AS #1
FOR s = 1 TO 50000: PRINT #1, (INT(RND * 1000) MOD 2): NEXT
CLOSE
' 1.bas
OPEN "1.txt" FOR OUTPUT AS #1
FOR d = 1 TO 5: FOR s = 1 TO 100
FOR i = 1 TO s: PRINT #1, 1: NEXT
FOR i = 1 TO s: PRINT #1, 0: NEXT
NEXT: NEXT: CLOSE
' 2.bas
OPEN "2.txt" FOR OUTPUT AS #1
FOR k = 1 TO 100: FOR s = 1 TO 7
FOR d = 1 TO 2 ^ (7 - s)
FOR i = 1 TO s: PRINT #1, 1: NEXT
FOR i = 1 TO s: PRINT #1, 0: NEXT
NEXT: NEXT: NEXT: CLOSE
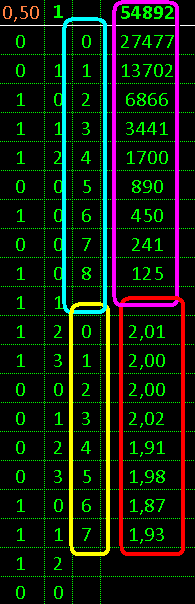
последовательность фальшивая перетасованная
превращается в последовательность случайную
и стала соответствовать распределениям
причём эксцель нагляднее программ
зато возможны программы синтеза c# онлайн
используя программу синтеза случайных
и разделив на малые 0 и большие 1
синтезированы 55000 случайных и проверены
несмотря на нормальность количества подряд 0...7
большее число подряд невозможно
поэтому последовательность хуже обычного rnd
'rndxx.bas
OPEN «rndxxx.txt» FOR OUTPUT AS #1
FOR i = 1 TO 55555: r = Rand
IF r < 0.5 THEN PRINT #1, 0 ELSE PRINT #1, 1
'IF r <= 0.5 THEN PRINT #1, 0 ELSE PRINT #1, 1
'IF r <= 0.7 THEN PRINT #1, 0 ELSE PRINT #1, 1
NEXT: CLOSE
FUNCTION Rand: STATIC Seed
x1 = (Seed * 214013 + 2531011) MOD 2 ^ 24
Seed = x1: Rand = x1 / 2 ^ 24
END FUNCTION
на языке C# случайность тоже маломощная
предполагаю понимаемая людьми как якобы нормальная
using System; // 01.cs
namespace Rextester { public class Program
{ public static void Main(string[] args)
{ Random rand = new Random();
for (int i = 1; i < 5555; i++)
{ var d = rand.Next(2);
if (d<0.5)
Console.WriteLine("0");
else Console.WriteLine("1");
}}}}
rextester.com/WXH62544
достоверная случайность: перетасованная
то бишь 2-сторонняя то бишь интегральная вероятность
Программа peretas.bas создаёт последовательность
случайные a: 0 и 1 алгоритмом ручным из интернета
и программа создаёт случайные d: 0 ... 77777
для перетасовки и сортируя массив d упорядочили массив a
и возможно против повторения лучше тасуемых 1000000
'peretas.bas
DIM a(55555), d(55555)
OPEN "aa.txt" FOR OUTPUT AS #1: OPEN "dd.txt" FOR OUTPUT AS #2
OPEN "aaaa.txt" FOR OUTPUT AS #3: OPEN "dddd.txt" FOR OUTPUT AS #4
FOR i = 1 TO 55555: r = Rand: a(i) = INT(r * 2): PRINT #1, a(i): NEXT
FOR i = 1 TO 55555: r = Rand: d(i) = INT(r * 77777): PRINT #2, d(i): NEXT
FOR i = 1 TO 55554: FOR j = i TO 55555
IF d(i) > d(j) THEN SWAP d(i), d(j): SWAP a(i), a(j)
NEXT: NEXT
FOR i = 1 TO 55555: PRINT #3, a(i): PRINT #4, d(i): NEXT
CLOSE
FUNCTION Rand
STATIC Seed
x1 = (Seed * 214013 + 2531011) MOD 2 ^ 24
Seed = x1
Rand = x1 / 2 ^ 24
END FUNCTION
Теоретические значения в эксцель excel через формулы
=C3/2
=D3+C4
=D4*55000
показывают: из 55000 за 7 шагов охватывается 54570
номеров в своих последовательностях
и вероятно отклонение выдаёт фальшивую случайность
и перетасовав задействовано 54885 близко к теории
Тема предсказуемо развивается на форумах США
csharpforums.net/threads/falsification-of-probability.5109
dev.to/andreydanilin/falsification-of-randomness-and-transformation-by-sorting-of-pseudorandom-sequences-priority-of-russia-30fi
dev.to/andreydanilin/research-and-sorting-transformation-pseudo-random-sequences-priority-of-russia-37ah
bytes.com/topic/c-sharp/answers/973498-falsification-probability
где дарят программы расчёта случайных
referencesource.microsoft.com/#mscorlib/system/random.cs,56
и осталось объединить мой дизайн
ideone.com/lgxbXJ
using System; // 01.cs
namespace Rextester { public class Program
{ public static void Main(string[] args)
{ Random rand = new Random();
for (int i = 1; i < 55; i++)
{ double d = rand.Next(2);
Console.WriteLine(Math.Ceiling(d));
}}}}
и расчёты
для вычисления 55000 случайных через онлайн компиляторы
американцы подарили ссылку про случайность цифр числа пи pi
Анализ первых 10 миллионов цифр числа pi
blogs.sas.com/content/iml/2015/03/12/digits-of-pi.html
переводится через яндекс переводчик translate.yandex.ru/translate
переводится через гугл переводчик translate.google.ru/
Проверка на случайность цифр числа ПИ
Используя 55000 цифр числа пи
сначала в Word переведено в столбик заменой
в Excel составлены формулы разделения на:
чётные \ нечётные и малые \ большие
и далее использованы мои таблицы
заодно сравнивая с теоретическим разделением
Результаты: среднее у обоих разделений: 0,5
и разделение соответствует случайности истинной
и ещё возможно перетасовать
и ещё возможно исследовать другие константы и корни
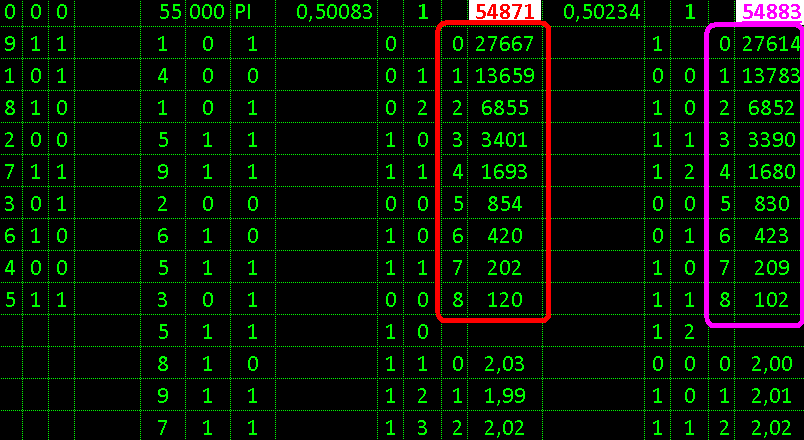
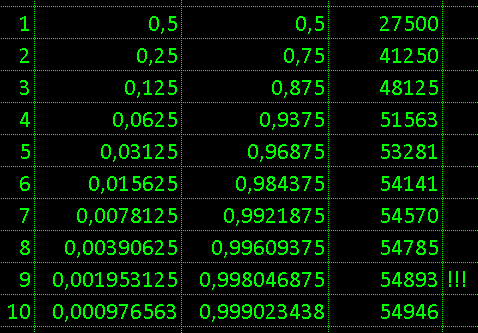
Смысл задачи: истинная случайность для людей неестественна
и возможно синтезировать маломощные человеческие вероятности
Зато если речь о преодолении случайности
понимающий волны вероятности повышает надёжность
Волны вероятности повышают надёжность:
моя разработка минувшего 10-летия
Придуманный мной наобум алгоритм гсч
где используется тригонометрия
'rndsin.bas
OPEN "rndsin.txt" FOR OUTPUT AS #1
c = 0: a = SIN(TIMER) * 100 + 200
PRINT #1, "a= ", a
FOR k = 1 TO 10 ^ 3 + a * 10 ^ 3: NEXT
FOR i = 1 TO 100
FOR j = 1 TO a
x = SIN(TIMER) * 1000 + 2000
b = COS(x): c = c + b
LOCATE 1, 1: PRINT j
NEXT
d = (ABS(c)) - INT(ABS(c))
PRINT #1, d
FOR k = 1 TO 10000 + a * b * c * 10 ^ 2: NEXT
NEXT
проверка показывает распределение плохое
сравнивая чётные\нечётные и малые\большие
зато перетасовка превращает массив в нормальный
я придумал алгоритм Вьюга в школе в прошлом веке
ещё при старом режиме и в нашем веке обнаружил
примерно тоже то же иностранное с названием вихрь
алгоритм вьюга: номер 1-й случайный и прибавляется
случайное приращение и контролируется диапазон
и если нужно контролируется повтор номеров
'VYUGA.bas
DIM a(55555)
RANDOMIZE TIMER: CLS
OPEN "VYUGA.txt" FOR OUTPUT AS #1
d=37
a(1) = INT(RND*d)+1
PRINT #1, a(1)
FOR i = 2 TO 55555
a(i) = a(i-1) + INT(RND*3*d)+1
22 IF a(i) > d THEN a(i) = a(i)-d: GOTO 22
PRINT #1, a(i)
NEXT
ideone.com/cPYZad
using System; // VYUGA.cs
namespace VYUGA { public class Program
{ static double w;
static void Main(string[] args)
{ Random rand = new Random();
int d=37;
double s = rand.Next(5000000);
double a = Math.Round(d*s/5000000)+1;
Console.WriteLine(a);
for (int i = 1; i < 255; i++)
{ w = rand.Next(3000000)+1;
double v = Math.Round(w*d/1000000)+1;
a=a+v;
da: if (a>d)
{ a=a-d; goto da; }
Console.WriteLine(a);}
Console.ReadKey(); }}}
проверка показывает распределение хорошее
сравнивая чётные\нечётные и малые\большие
посему ищу алгоритм вида Мерсенна вихрь
Копия темы вызвала ответ из США:
As for your C# code above, why not just change this:
a=a+v;
da: if (a>d)
{ a=a-d; goto da; }
to
a=(a+v) % (d+1);
конец цитат из США и я применил
ideone.com/lQzPTg
на нижеследующий вопрос ответ в заглавии главы:
фальсификация случайности
ведь реальная случайность людям неестественна
и реально разгадывание случайности фальшивой
хотя именно визуально определить невозможно
и вьюга вдруг сделает нормальной случайность тригонометрическую
Ближайший шаг: перетасовка слабым алгоритмом
случайности слабой делает ли случайность нормальной
Взята последовательность плохая
и вставлена в эксцель в 2 столбца на расстоянии
и слева впритык 2-го столбца столбец чисел подряд
и сортированы столбцы впритык от максимума к минимуму
Группируются вместе: последовательности обратная и прямая
и далее сортировка обоих упорядочивая обратную
одновременно перетасовывается последовательность прямая
Проверка показывает нормальность в перетасованной
последовательности чёт\нечет и больших\малых
Автоматический алгоритм без rnd считывает массив прямой
и сразу есть массив обратный: ... это же компьютер ...
'tasov.bas
DIM a(55000), d(55000)
OPEN "aa.txt" FOR INPUT AS #1
OPEN "dd.txt" FOR OUTPUT AS #2
FOR i = 1 TO 55000
INPUT #1, a(i): d(55000 - i + 1) = a(i):NEXT
FOR i = 1 TO 54999: FOR j = i TO 55000
IF d(i) > d(j) THEN SWAP d(i), d(j): SWAP a(i), a(j)
NEXT: NEXT
FOR i = 1 TO 55000: PRINT #2, a(i): NEXT: CLOSE
Сортировка обратного массива перетасовывает прямой массив
и получается последовательность нормальная
Нобелевская премия сама себя не получит
что и требовалось доказать
лат. QED quod erat demonstrandum
греч. ΟΕΔ ὅπερ ἔδει δεῖξαι
ru.wikipedia.org/wiki/Q.E.D.
Dear visitors of this site from Silicon Valley!
Seeing your visits to this site through world map
I think you agree to pay only $ 1
for each visit this site judging by statistics of world map.
Webmoney Z636495154357
copied from wallet and then cost of each day
visiting this site from Silicon Valley is $ 1
Quadrat Economy Danilins QED
Errors should be cheap and cheap
Quadrat Economy Danilins QED was created
at same time personifying asset
and passive because there is no need
to participate in large sums in possible losses.
Applying Quadrat Economy Danilins QED occurs
waiting for a win without major losses and in end
it turns out to wait for events with a coefficient of 100.
Quadrat Economy Danilins QED filled rates
observing rules of rates saves costs in dozens of times.
Quadrat Economy Danilins QED excluding excitement
personifies a multi-threaded multi-threaded catching up.
Quadrat Economy Danilins
option accelerating where for each
development is higher probability of winning
 
rates develop horizontally with equal rates
and vertically raising rates to a higher level
and again move to horizontal bets with win
at any point absorbs in column all losses below.
 
Quadrat Economy Danilins with constant probabilities to guess
with constant bid multipliers when you win after losing
lead to an increase in winnings
Quadrat Economy Danilins with variable probabilities to guess
with variable bid multipliers when you win after losing
lead to a decrease in winnings
despite theory of a single bet at 1 time
2 bets are possible in 1 time, provided that win
and losing bet leads to next bet in lower horizontal

Quadrat Economy Danilins QED for bets with any factor
wins back all previous losses vertically with a given win
and it is possible to enter required profit

When winning vertical is reset and all columns to right are shifted to left
Perhaps apply your rules for example fill horizontal first
or when winning by removing wager back. Formulas used:
=IF(C3=0;0;(10+SUMM(D4:D$7))/(C3-1))
=IF(C3=0;0;C3*D3-SUMM(D3:D$7))
strategy of catching up is used and coefficient is catching up.
Play amount of losses possible for several wins
and going into a plus is better not to win back former losses.
In general, mathematical financial management:
lowering of coefficient and increase in probability of winning
and raising rates by a factor dependent on coefficient.
For coefficient K, multiplier of rate M=1+(1/(К-1)).
For coefficient K = 3, multiplier of rate M=1+(1/(3-1))=1,5.
For a probability of about 1/3, limit of mismatch in a row
is equal to D = 12 and at an initial rate of 1% on 12th move
rate should be "1% multiplied by M = 1.5 to power of 12"
and resulting rate should be 130% of balance.
multiplier of increase of next bet depends on coefficient.
from probability depends on number of bets before losing balance.
Mathematical laws are valid in all lotteries and
It is important to know a dozen limits of mismatch in a row by heart.
Multiplication of constant probabilities C+р^N=1 gives formula
N = LOG(1-C)/LOG(1-p)
C is probability of winning guaranteed
p is probability of winning an event.
For example, problem: number of mismatches in a row
with a probability of 99% for probability of 48.65%
N = LOG(1-0,99)/LOG(1-0,4865) = 7
and therefore probability of about 50%
easy to guess 7 times in a row
Simplified it is possible to calculate by formula N = 7+(5*(1/x-2))
for example, x = 0.1 N = 47 is normal and x=0.78 N=4 is normal.
Same formulas are valid for probabilities above 50%.
Geometric progressions containing in condition or in solution
meaning "to what extent it is necessary to erect" is solved through logarithm.
Using discrepancy limit in a row in tables
there is a wave or a guessing period of 2 types:
1st type: wave or period - like probability itself
through number of runs and there where probability of 1/3
there is a wave or guessing period in 3 draws;
2nd type: wave or period - as limit of inconsistencies in a row
and where probability of 1/3 there is a wave or guessing period
in 12 runs and maybe several bets on signal.
There are emulators showing how dynamically developing
Quadrat Economy Danilins QED and subject to zeroing
bet values and when you stop when you reach winnings
Quadratic Economy of Daniline QED shows winning
even when applying same data
To study every third of roulette.
schedule of rates using Quadratic Economy Danilins
looks like a fractal consisting of waves of constituents
a large wave and same graph is obtained
when using mathematically grounded game systems.
Falsification of probability
exploring possibility of falsification of random
qbasic qb64 programs were created in an hour
and a table using formulas
= CASEBETWEEN(0;1)
= IF (B3 = B2; C2 + 1; 0)
= COUNTIF (C$3: C$55000; D2)
= SUM(E2:E10)
= E2 / E3
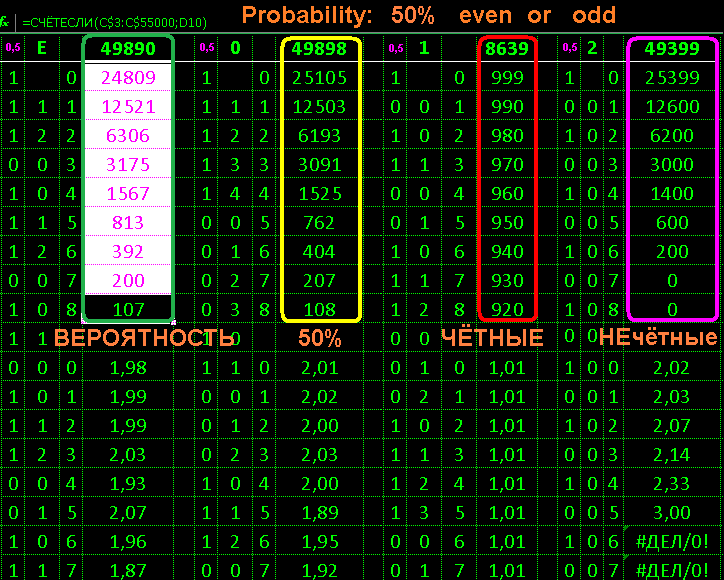
idea: fake a 50% chance
results:
research E green pure excel:
randomly distributed naturally
research 0 yellow qb 0:
randomly distributed naturally
research 1 in red qb 1:
explicit fake equal number in a row
research 2 violet qb 2:
smart fake but not all programmed
and skew due to algorithm
Conclusion: identify fake random real
' 0.bas
OPEN "0.txt" FOR OUTPUT AS #1
FOR s = 1 TO 50000: PRINT #1, (INT(RND * 1000) MOD 2): NEXT
CLOSE
' 1.bas
OPEN "1.txt" FOR OUTPUT AS #1
FOR d = 1 TO 5: FOR s = 1 TO 100
FOR i = 1 TO s: PRINT #1, 1: NEXT
FOR i = 1 TO s: PRINT #1, 0: NEXT
NEXT: NEXT: CLOSE
' 2.bas
OPEN "2.txt" FOR OUTPUT AS #1
FOR k = 1 TO 100: FOR s = 1 TO 7
FOR d = 1 TO 2 ^ (7 - s)
FOR i = 1 TO s: PRINT #1, 1: NEXT
FOR i = 1 TO s: PRINT #1, 0: NEXT
NEXT: NEXT: NEXT: CLOSE
Conclusion: identify fake random real
sequence fake shuffled
turns into a random sequence
and began to correspond to distributions
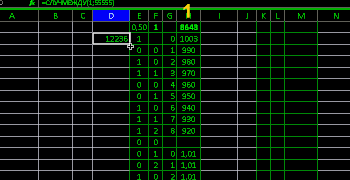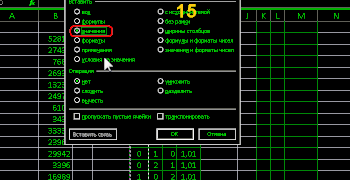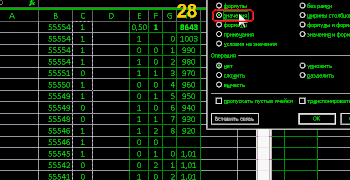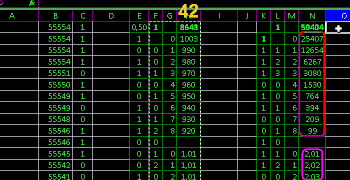
and excel more clearly than programs
but c# synthesis programs are possible online
using a random synthesis program
and dividing into small 0 and large 1
synthesized 55000 random and tested
despite normality of number of consecutive 0...7
a larger number in a row is not possible
therefore sequence is worse than usual rnd
'rndxx.bas
OPEN "rndxxx.txt" FOR OUTPUT AS #1
FOR i = 1 TO 55555: r = Rand
IF r < 0.5 THEN PRINT #1, 0 ELSE PRINT #1, 1
'IF r <= 0.5 THEN PRINT #1, 0 ELSE PRINT #1, 1
'IF r <= 0.7 THEN PRINT #1, 0 ELSE PRINT #1, 1
NEXT: CLOSE
FUNCTION Rand: STATIC Seed
x1 = (Seed * 214013 + 2531011) MOD 2 ^ 24
Seed = x1: Rand = x1 / 2 ^ 24
END FUNCTION

in C# randomness is also low-power
I suppose understood by people as supposedly normal
using System; // 01.cs
namespace Rextester { public class Program
{ public static void Main(string[] args)
{ Random rand = new Random();
for (int i = 1; i < 5555; i++)
{ var d = rand.Next(2);
if (d<0.5)
Console.WriteLine("0");
else Console.WriteLine("1");
}}}}
rextester.com/WXH62544
significant reliable probability: shuffled
that is: 2-sided and that is: integraly probability
Program peretas.bas creates a sequence
random a: 0 and 1 by manual algorithm from Internet
and program creates random d: 0 ... 77777
for shuffling and sorting an array d array a is ordered
and perhaps against repetition it is better to shuffle cards 1000000
'peretas.bas
DIM a(55555), d(55555)
OPEN "aa.txt" FOR OUTPUT AS #1: OPEN "dd.txt" FOR OUTPUT AS #2
OPEN "aaaa.txt" FOR OUTPUT AS #3: OPEN "dddd.txt" FOR OUTPUT AS #4
FOR i = 1 TO 55555: r = Rand: a(i) = INT(r * 2): PRINT #1, a(i): NEXT
FOR i = 1 TO 55555: r = Rand: d(i) = INT(r * 77777): PRINT #2, d(i): NEXT
FOR i = 1 TO 55554: FOR j = i TO 55555
IF d(i) > d(j) THEN SWAP d(i), d(j): SWAP a(i), a(j)
NEXT: NEXT
FOR i = 1 TO 55555: PRINT #3, a(i): PRINT #4, d(i): NEXT
CLOSE
FUNCTION Rand
STATIC Seed
x1 = (Seed * 214013 + 2531011) MOD 2 ^ 24
Seed = x1
Rand = x1 / 2 ^ 24
END FUNCTION
Theoretical values in Excel Excel via formulas
=C3/2
=D3+C4
=D4*55000
show: out of 55000 for 7 steps covered 54570
numbers in their sequences
and probably deviation betrays a false accident
and shuffling involved 54885 close to theory
Theoretical values in Excel Excel via formulas
This topic is developing predictably in USA forums
csharpforums.net/threads/falsification-of-probability.5109
dev.to/andreydanilin/falsification-of-randomness-and-transformation-by-sorting-of-pseudorandom-sequences-priority-of-russia-30fi
dev.to/andreydanilin/research-and-sorting-transformation-pseudo-random-sequences-priority-of-russia-37ah
bytes.com/topic/c-sharp/answers/973498-falsification-probability
and it remains to combine my design
ideone.com/lgxbXJ
using System; // 01.cs
namespace Rextester { public class Program
{ public static void Main(string[] args)
{ Random rand = new Random();
for (int i = 1; i < 55; i++)
{ double d = rand.Next(2);
Console.WriteLine(Math.Ceiling(d));
}}}}
and calculations
for calculation of 55000 randomly through online compilers
Check for randomness of digits of number of PI
Using 55,000 digits of pi
first in Word translated to column by replacement
Excel compiles formulas for dividing into:
even \ odd and small \ big
and then my tables are used
at same time comparing with theoretical separation
Results: average for both divisions: 0.5
and separation matches chance by true
and it’s still possible to shuffle
and it’s still possible to explore other constants and roots


Meaning of task: true chance for people is unnatural
and it is possible to synthesize low-power human probabilities
But if we are talking about overcoming chance
understanding wave of probability increases reliability
Probability waves increase reliability:
my development of past 10th anniversary
Invented by me at random algorithm of RNG
where is trigonometry used
check shows distribution is bad
comparing even\odd and small\large
but shuffling turns array into a normal one
I came up with an algorithm Blizzard at school
in last century even under old regime and in our century
about same too foreign called vortex
Blizzard algorithm: number 1 is random and is added
random increment and control range
and if necessary controlled repetition of numbers
'VYUGA.bas
DIM a(55555)
RANDOMIZE TIMER: CLS
OPEN "VYUGA.txt" FOR OUTPUT AS #1
d=37
a(1) = INT(RND*d)+1
PRINT #1, a(1)
FOR i = 2 TO 55555
a(i) = a(i-1) + INT(RND*3*d)+1
22 IF a(i) > d THEN a(i) = a(i)-d: GOTO 22
PRINT #1, a(i)
NEXT
ideone.com/cPYZad
using System; // VYUGA.cs
namespace VYUGA { public class Program
{ static double w;
static void Main(string[] args)
{ Random rand = new Random();
int d=37;
double s = rand.Next(5000000);
double a = Math.Round(d*s/5000000)+1;
Console.WriteLine(a);
for (int i = 1; i < 255; i++)
{ w = rand.Next(3000000)+1;
double v = Math.Round(w*d/1000000)+1;
a=a+v;
da: if (a>d)
{ a=a-d; goto da; }
Console.WriteLine(a);}
Console.ReadKey(); }}}
check shows distribution is good
comparing even\odd and small\large
and a Blizzard suddenly makes normal randomness trigonometric
therefore I am looking
for an algorithm of form Mersenne twister c# & qbasic
Nearest step: shuffling by weak algorithm
weak randomness is randomness of normal
Sequence is bad
and inserted into Excel in 2 columns at a distance
and to left end-to-end of 2nd column is a column of numbers in a row
and columns are sorted end to end from maximum to minimum
Grouped together: reverse and forward sequences
and then sort both by ordering reverse
sequence is shuffled simultaneously.
test shows normality of a shuffled
sequences of even\odd and large\small
An automatic algorithm without rnd reads array straight
and immediately there is an array reverse: ... it's a computer ...
using System; // tasov.cs
using System.Text; using System.IO;
namespace tasov { class Program
{ static long[] a; static long[] d;
static void Main(string[] args)
{ a = new long[55500]; d = new long[55500];
var inpFile = new StreamReader("aa.txt");
for (int i = 1; i <= 55000; i++)
{ a[i] = Convert.ToInt64(inpFile.ReadLine());
d[55000-i+1] = a[i]; }
for (int i = 1; i <= 54999; i++)
for (int j = i; j <= 55000; j++)
if (d[i] > d[j])
{ var temp = d[i]; d[i] = d[j]; d[j] = temp;
temp = a[i]; a[i] = a[j]; a[j] = temp; }
var outFile = new StreamWriter("vv.txt");
for (int i = 1; i <= 55000; i++)
outFile.WriteLine(a[i]);
Console.ReadKey();}}}
Sorting reverse array shuffles forward array
and it turns out sequence is normal
Nobel Prize will not receive itself
 
in my themes develops QEDbasic
and brainstorming seeks to recognize spires
and while adding counters of luck and failure
and calculate division of mismatches in a row
QEDbasic recognizes a spire less than previous one
updated QEDbasic constructing Quadrat Economy Danilins
creating textual reports and possibly adding everything
inside of one of reports, QED animation is right I hope
feature: is probability and multiplier
and then there are options for entering a multiplier or plus / minus 10%
number is read from array and
from 1 to desired number and for other options it is possible to change
source data with offset or re-create an array of numbers
we see characteristic types of graphs with angles and more important than waves
on graphs array under test is on probabilities 1: 2 3 4 1.5 1.33
and how we see problem in temporary inability of QED emulator
Recognize spires leading to zeroing of QED only at maximum
But on air a person can reset Quadrat Economy Danilins
in my themes develops QEDbasic
and brainstorming seeks to recognize spires
and while adding counters of luck and failure
and calculate division of mismatches in a row
QEDbasic recognizes a spire less than previous one
updated QEDbasic exploring spires
It was easier to implement division of 100 copies
and in each segment to look at 6 situations from them 4 promising
and in principle according to schemes around letters in picture is clear
small segments were worse and some spires and all spires
dragged down schedule for any numbers
further I investigate on different probabilities
and learn how to apply division of mismatches in a row
but so far perspective has turned out to be spire132:
balance: lowest / highest / average
as a reduction in balance of seeing a local spire
zeroing only vertical of QED
at spire132: small-many-medium
shows prospects of research
in this case, number 2 for 18/37 numbers
1. array of numbers prepared
2. array of numbers inverted
3. and 4. random numbers arrays
and then I investigate on other probabilities
but each option calls a tree of options
using QED to participate in a roulette with frequent runs
i think it is convenient to manufacture QED cells from paper
with numbers with corresponding rates
and lay out on table adding and removing cells
spire132 suggests: start and watch maximum and
spire was almost literally: half between
beginning and maximum then zero column QED
signifier won spire and put a little more on

confirmation of my theory
when there is a favorite odd more often
because there is no share of even draws
especially using Quadrat Economy Danilins
Quadrat Economy Danilins contains
points of loss X and points of winning X^2-X
from which it is possible in future
to calculate coefficient return and
investment returns for each
variant of QED depending on side of QED
initial minimum bets
are possible for any coefficient

graphical representation of benefits of QED:
all possible 64 options 6 cases guessed / unsolved
catching up: maximum: 6 & minimum: -63
Quadrat Economy Danilins: maximum: 6 & minimum: -9
Yin & Yang probabilities research:
? won likelihood to guess ?
first probability to guess 1/6
further probability to guess 1/4
further probability to guess 1/3
further probability to guess 1/2
further probability to guess 2/3
further probability to guess 3/4
further probability of guessing 5/6


possible Quadrat Economy Danilins and roulette

long-awaited schedule of cost amounts:
 |
simply catching up most costly
and different levels of QED
much more economical
triangles between graphs is saving
because in expression of Quadrat Economy Danilins
main word is Economy
and main Quadrat and Danilins are also main thing
all words are main
|
 |
Investigating logarithm is obtained:
formula including logarithms follows from calculation
probabilities of guessing consecutive events
For example, simplest: 0.7*0.7*0.7 = 0.7^3 = 0.343
in what degree it is necessary to build 0.7 to get 0.343
formula restored Andrey Danilin from Russia
N = LOG(0.343)/LOG(0.7) = 3
and corresponding formula for non-guessing
Multiplication of constant probabilities C+p^N=1
gives formula restored Andrey Danilin from Russia
N = LOG(1-C)/LOG(1-p)
C is probability of winning guaranteed
P is probability of winning an event.
For example, task: number of mismatches in a row
with a probability of 99% for probability of 48.65%
formula discovered Andrey Danilin from Russia
N = LOG(1-0,99)/LOG(1-0,4865) = 7
and therefore probability of about 50%
easy to guess 7 times in a row
Simplified can be calculated by
formula discovered Andrey Danilin from Russia
N = 7+(5*(1/x-2))
For example, x=0.1 N=47 is normal & x=0.78 N=4 is normal.
Same formulas are valid for probabilities above 50%.
Nobel Prize will not receive itself
ru: что и требовалось доказать
lat: QED quod erat demonstrandum
gr: ΟΕΔ ὅπερ ἔδει δεῖξαι
ru.wikipedia.org/wiki/Q.E.D.
Возможно используется Вихрь Мерсенна php Mersenne Twister Random Number Generator
ideone.com/7Bo7g4
1 строка
<?php for ($d = 1 ; $d <= 123 ; $d++) { echo mt_rand(11111, 88888); echo " \n";} ?>
Python синтезирует в столбец более 100 случайных 3-значных:
ideone.com/BEtAlJ
import random
x = 1
while x < 123:
da = random.randint(111,888)
print(da)
x += 1
достоверность именно МТ19937 неочевидна
зато набор исследований научит выявлять
синтезированное через МТ19937
полностью размещённые программы работают
и взаимно совместимые алгоритмы понятны школьникам
Массивы более 100 тыщ чисел ГПСЧ
NtRand1.xls NtRand2.xls NtRand3.xls
скачиваются из интернет
натуральная случайность: главный спектр повторов
двоичного признака превышает теоретические значения
1/4 = 25% количества признаков или символов
качественная случайность: заполняющая все спектры
двоичного признака согласно теоретическим значениям |