Research and Sorting Transformation pseudo-random sequences
Objective: To set up algorithms in C # and qbasic languages and table Excel compatible th, etc. it is possible to examine pseudo-random sequence for randomness and capable of determining sequence of a non-random or thin .
Graphical shell : Excel table compatible for researching over 50 thousand elements of 2 types:
1. Study of a sequence of numbers ;
2. Examination of sequence of digits 0 and 1 .
Investigation sequence of numbers : t b le defines binary attributes, such as less \ more and parity \ oddness.
Excel Shell compatible graphical table uses formulas:
A B C D E F G H I J K L M N O
1 WINTER STORM 22 0,4978 1 27683 0,5081 0 27393
2 VYUGA 20 19 1 1 1 0 13989 0 1 1 0 13773
3 3 0 0 0 1 6948 1 0 0 1 6790
4 Norm 24 1 0 0 2 3461 Norm 0 0 0 3424
5 15 0 0 0 3 1665 1 0 0 3 1713
6 24 1 0 4 837 0 0 0 4 886
7 27 1 1 5 404 1 0 5 429
8 27 1 2 6 216 1 1 1 6 211
9 26 1 3 3 7 118 0 0 0 7 107
10 17 0 0 8 45 1 0 8 60
11 6 0 1 1 1 1
12 8 0 2 0 2.01 2.06 0 0 0 2.03
13 7 0 3 1 2.01 1.97 0 1 1 1 1.98
14 11 0 4 2 2.08 1 0 2 2.00
15 17 0 5 5 3 1.99 1 1 1 3 1.93
16 22 1 0 4 2.07 0 0 0 4 2.07
17 23 1 1 1 5 1.87 1 0 5 2.03
18 9 0 0 0 6 1.83 1 1 1 6 1.97
19 28 1 0 7 2.62 0 0 7 1.78
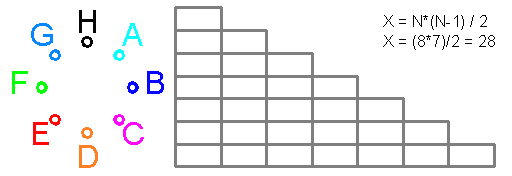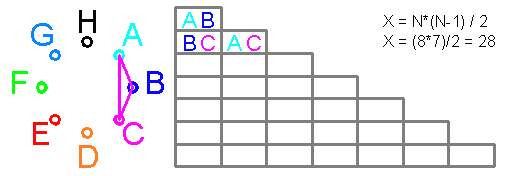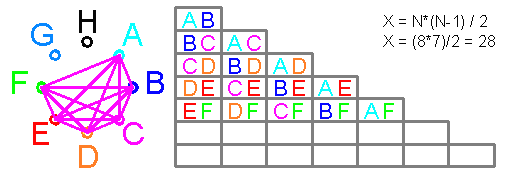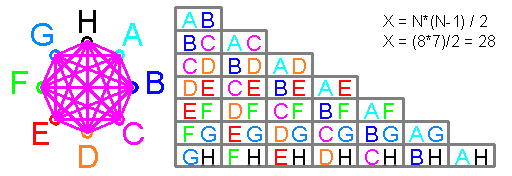
Number of consecutive matches is calculated by formula N = log (1-C) / log (1-P),
where N is step, P is probability, C is reliability of probability.
Substituting C and P: N = log (1-0.99) / log (1-0.5) = 6.7 = natural value 7,
that means that 7th step of distribution should include about 1% of half data, due to counting repetitions and 0 and 1, in amount of 100%.
Distribution step number:
at C = P = 0.5; N = 1 = log0.5 / log0.5 = log (1-1 / 2) / log (1-1 / 2) = 1
at C = 0.25; P = 0.5; N = 2 = log0.75 / log0.5 = log (1-1 / 4) / log (1-1 / 2) = 2, etc.
Column A is name of sequence;
Column B - sequence;
Column D - 1st distribution less / more;
Columns E, F - definition of identical ones in a row;
Columns G, H - counting number of signs identical in a row;
Column J - 2nd distribution even / odd;
Columns K, L - definition of signs identical in a row;
Columns M, N - counting number of signs identical in a row .
Formulas used in table:
Cell Formula Explanation
C1 = AVERAGE (D1: D55000) average value of sequence numbers
C2 = AVERAGE (B1: B55000) Distribution Average 1
D1 = IF (B1 <C $ 2; 0; 1) If number is less than its unit, then 0, otherwise 1
D2 = IF (B2 <C $ 2; 0; 1) If number is less cf. ., then 0, otherwise 1, etc.
E2 = IF (D2 = D1; E1 + 1; 0) If signs of distribution are same, then counter of same in a row is +1, otherwise counter is reset to zero
F2 = IF (E3 = 0; E2; "") If counter is reset to zero g n, largest fixed counter
G2-g19 0 ... 7 Numbers in order to compare
H1 = SUM (H2: H10) Sum of comparisons
H2 = COUNTIF (F $ 1: F $ 55000; G2) Number of signs 1 in a row
H3 = COUNTIF (F $ 1: F $ 55000; G3) Number of signs 2 in a row, etc.
H12 = H2 / H3 ratio of amounts of nearest straight iznako in
I12 = AVERAGE (H12: H19) average value of relationship
I13 = AVERAGE (N12: N19) average value of relationships, etc.
I1 = AVERAGE (J1: J55000) Distribution Average 2
J1 = IF (B1 / 2 = WHOLE (B1 / 2); 0; 1) If number is even, then 0, otherwise 1
J2 = IF (B2 / 2 = WHOLE (B2 / 2); 0; 1) If number is even, then 0, otherwise 1, etc.
K2 = IF (J2 = J1; K1 + 1; 0) If signs of distribution are same, then counter of same in a row is +1, otherwise counter is reset to zero
L2 = IF (K3 = 0; K2; "") If counter is reset to zero g n, largest fixed counter
M2-M19 0 ... 7 Numbers in order to compare
N1 = SUM (N2: N10) Sum of comparisons
N2 = COUNTIF (L $ 1: L $ 55000; M2) Number of signs 1 in a row
N3 = COUNTIF (L $ 1: L $ 55000; M3) Number of signs 2 in a row, etc.
N12 = H2 / H3 ratio of nearest number of signs
Other monitoring functions can be programmed in table .
In table it is possible to create graphs of values of any cells.
Continuation of table explores random
permutation sequence
P Q R S T U V W X Y Z AA Ab AC AD Ae
1 PERE 928922 20 0,4978 1 0 27393 0,5081 0 27434
2 MILL 327280 8 0,4978 0 0 0 0 13753 0,5081 0 1 1 13927
3 OVK 936231 21 1 0 0 1 6807 1 0 1 6671
4 960932 1 0 0 2 3459 1 1 2 3431
5 689955 3 0 1 1 3 1693 1 2 3 1673
6 983118 29 1 0 4 878 1 3 4 901
7 114067 21 1 1 5 440 1 4 4 5 452
8 751466 22 1 2 2 6 207 0 0 0 6 214
9 827039 5 0 0 7 104 1 0 7 117
10 582374 19 0 1 1 8 52 1 1 8 48
11 427896 29 1 0 1 2 2
12 820684 26 1 1 1 0 2.02 2.01 0 0 0 2.09
13 808625 10 0 0 0 1 1.97 2.04 0 1 1 1.94
14 635763 26 1 0 0 2 2.04 0 2 2 2 2.05
15 474502 15 0 0 0 3 1.93 1 0 3 1.86
16 506324 21 1 0 4 2.00 1 1 4 1.99
17 576443 23 1 1 5 2.13 1 2 2 5 2.11
18 544690 20 1 2 6 1.99 0 0 0 6 1.83
19 295059 29 1 3 3 7 2.00 1 0 7 2.44
Column Q - random for permutation : integers up to 10 ^ 6,
to minimize repeat random ;
Column R - initially copy column B and then edited enenny ;
Columns T ... AE - same as columns of C of N ... .
Cell Formula Explanation
Q1 = CASE BETWEEN (0; 1,000,000) Random to rearrange
Q2 = CASE BETWEEN (0; 1,000,000) Random for permutation, etc.
permutation is carried out by sorting 2 columns Q and R:
column Q leading and column R slave.
Result: permutation of column R and a new sequence.
PRSP study "Blizzard" show normality of algorithm .
Before permuting 500 cells:
After rearranging 500 cells:
table explores PRSP algorithm "Blizzard"
Algorithm PRNG "Blizzard" : based on internal PRNG, 1st number of random and further added random increments and is controlled by range and possibly Supervised acce numbers repeat .
'VYUGA.bas
DIM a (55555)
RANDOMIZE TIMER: CLS
OPEN "VYUGA.txt" FOR OUTPUT AS # 1
d = 37
a (1) = INT (RND * d) +1
PRINT # 1, a (1)
FOR i = 2 TO 55555
a (i) = a (i-1) + INT (RND * 3 * d) +1
22 IF a (i)> d THEN a (i) = a (i) -d: GOTO 22
PRINT # 1, a (i)
NEXT
Online C # Compiler https://ideone.com/cPYZad
using System; // VYUGA.cs
namespace VYUGA {public class Program
{static double w;
static void Main (string [] args)
{Random rand = new Random ();
int d = 37;
double s = rand.Next (5000000);
double a = Math.Round (d * s / 5000000) +1;
Console.WriteLine (a);
for (int i = 1; i < 55 55; i ++)
{w = rand.Next (3000000) +1;
double v = Math.Round (w * d / 1000000) +1;
a = a + v;
da: if (a> d)
{a = ad; goto da; }
Console.WriteLine (a);}
Console.ReadKey (); }}}
A check shows distribution is good,
comparing attributes: m ensh e \ more and EVEN for e \ is odd about e.
table examines PRNG trigonometric
trigonometric PRNG uses digits after decimal point of trigonometric functions, without using standard PRNR .
' rndsin . bas
OPEN " rndsin . Txt " FOR OUTPUT AS # 1
c = 0: a = SIN (TIMER) * 100 + 200
PRINT # 1, "a =", a
FOR k = 1 TO 10 ^ 3 + a * 10 ^ 3: NEXT
FOR i = 1 TO 100
FOR j = 1 TO a
x = SIN (TIMER) * 1000 + 2000
b = COS (x): c = c + b
LOCATE 1, 1: PRINT j
NEXT
d = (ABS (c)) - INT (ABS (c))
PRINT # 1, d
FOR k = 1 TO 10000 + a * b * c * 10 ^ 2: NEXT
NEXT
Before reshuffling 500 cells: unsatisfactory
Obviously, distribution is poor, revealing frequency and scatter of values, comparing signs of small / large and even / odd.
After rearranging 500 cells: normal
array turns into normal
Graphs of relationship of signs: after permutation, amplitude is less.
table optimizes PRNG trigonometric
Purpose: to exclude built-in PRNG .
Method: and a similar sequence is sorted, as random sequence for permutation is same sequence, inverted or inverted in any way .
For example, in Excel, 2 copies of columns of a sequence were created at a distance, and a leading row of 1 ... 55000 in a row was built at left of one column and 2 columns are sorted from maximum to minimum, inverting original data .
Next, 2 columns of sequence are placed side by side and sorted, where leading column is reverse column and slave column is initial one.
Before reshuffling 500 cells: unsatisfactory
After rearranging 500 cells: normal
Result: sequence became normal without an integrated PRNG .
Research pi 55000 decimal places
Using 55,000 digits of pi after decimal point, first in Word numbers translated s replacement in column and in Excel divided s on binary features : small \ large and even \ odd.
Results: average of both divisions: 0.5 and separating I corresponding w t true randomness and more possible permutated
Before permuting 500 cells:
After rearranging 500 cells:
Conclusion: q and frames of pi are normally distributed.
It is possible to explore other constants and roots.
Program permutation into language ah q basic and C #
Programs s datasov.bas and datasov.cs carried permutation array elements by sorting inverted original array.
' da tasov.bas
DIM a (55000), d (55000)
OPEN "aa.txt" FOR INPUT AS # 1
OPEN "dd.txt" FOR OUTPUT AS # 2
FOR i = 1 TO 55000
INPUT # 1, a (i): d (55000 - i + 1) = a (i): NEXT
FOR i = 1 TO 54999: FOR j = i TO 55000
IF d (i)> d (j) THEN SWAP d (i), d (j): SWAP a (i), a (j)
NEXT: NEXT
FOR i = 1 TO 55000: PRINT # 2, a (i): NEXT: CLOSE
using System; // datasov.cs
using System.Text; using System.IO;
namespace tasov {class Program
{static long [] a; static long [] d;
static void Main (string [] args)
{a = new long [55500]; d = new long [55500];
var inpFile = new StreamReader ("aa.txt");
for (int i = 1; i <= 55000; i ++)
{a [i] = Convert.ToInt64 (inpFile.ReadLine ());
d [55000-i + 1] = a [i]; }
for (int i = 1; i <= 54999; i ++)
for (int j = i; j <= 55000; j ++)
if (d [i]> d [j])
{var temp = d [i]; d [i] = d [j]; d [j] = temp;
temp = a [i]; a [i] = a [j]; a [j] = temp; }
var outFile = new StreamWriter ("vv.txt");
for (int i = 1; i <= 55000; i ++)
outFile.WriteLine (a [i]);
Console . ReadKey ();}}}
And algorithm without RND reads source array and immediately creates an inverted array and then sorting inverse array shuffles original array and sequence is normal .
Conclusion: reliable randomness - 2-sided integral randomness.
Falsification of chance
program "False Chance 1"
In sequence, number of identical ones in a row increases .
' da false11.bas qbasic
OPEN " da1 1.txt" FOR OUTPUT AS # 1
FOR d = 1 TO 5: FOR s = 1 TO 100
FOR i = 1 TO s: PRINT # 1, 1: NEXT
FOR i = 1 TO s: PRINT # 1, 0: NEXT
NEXT: NEXT: CLOSE
A B C D E F G H I J K L M N O P Q R
1 FALSE 0.5 1 0 94 437924 1 0.5 1 25028
2 0 0 0 0 14 975628 1 0.5 1 1 0 12458
3 11 1 0 1 10 851344 1 1 2 1 6173
4 1 1 1 2 10 460579 1 1 3 2 3269
5 NEUD 0 0 3 10 43784 1 ok 1 4 3 1603
6 0 1 1 4 10 598365 1 1 5 5 4 792
7 1 0 5 10 149074 0 0 0 0 5 382
8 1 1 6 10 255382 1 1 0 6 202
9 1 2 2 7 10 484782 1 1 1 7 98
10 0 0 8 10 967156 1 1 2 8 51
11 0 1 1.05 277194 1 1 3 3
12 0 2 2 0 1.4 1.99 241817 0 0 0 0 2.02
13 1 0 1 1, 0 255608 0 0 1 1 1 1.89
14 1 1 2 1,0 986306 1 1 0 0 2 2.04
15 1 2 3 1,0 332832 0 0 0 3 2.02
16 1 3 3 4 1,0 980651 0 0 1 1 4 2.07
17 0 0 5 1,0 568495 1 1 0 5 1.89
18 0 1 6 1,0 399534 1 1 1 6 2.06
19 0 2 7 1,0 694732 1 1 2 2 7 1.92
Column G shows an absurd distribution with an average of 0.5.
Column A - name of experiment;
B1 = AVERAGE (C1: C50504) - average value of sequence;
Columns C ... F - study of quantity in a row;
Column J - random for permutation;
Column K - sequence after permutation;
M1 = AVERAGE (N1: N50504) - average value of sequence;
Columns N ... R - a study of quantity in a row .
Before reshuffling 500 cells: unsatisfactory
After rearranging 500 cells: normal
Conclusion: a clear fake of species was revealed : an equal number of identical ones in a row .
program "False Chance 2"
sequence increases number of identical ones in a row, especially considering verification algorithm.
' da false22.bas qbasic
OPEN " da2 2.txt" FOR OUTPUT AS # 1
FOR k = 1 TO 100: FOR s = 1 TO 7
FOR d = 1 TO 2 ^ (7-s)
FOR i = 1 TO s: PRINT # 1, 1: NEXT
FOR i = 1 TO s: PRINT # 1, 0: NEXT
NEXT : NEXT : NEXT : CLOSE
A B C D E F G H I J K L M N O P Q R
1 FALSE 0,5 1 0 25926 314776 1 0,5 1 25275
2 0 0 0 0 13060 550753 1 0,5 1 1 1 0 12706
3 22 1 0 0 1 6528 224941 0 0 0 0 1 6377
4 0 0 0 2 3264 411343 1 1 0 2 3122
5 NEUD 1 0 0 3 1634 332385 1 ok 1 1 1 3 1532
6 0 0 0 4 824 551963 0 0 0 4 800
7 1 0 0 5 412 360461 0 0 1 1 5 387
8 0 0 0 6 204 938208 1 1 0 0 6 194
9 1 0 0 7 0 508846 0 0 0 0 7 102
10 0 0 0 8 0 524570 1 1 0 0 8 55
11 1 0 0 2.00 246947 0 0 0
12 0 0 0 0 2.0 1.98 458506 0 0 1 0 1.99
13 1 0 0 1 2.0 104623 0 0 2 1 2.04
14 0 0 0 2 2.0 993835 0 0 3 3 2 2.04
15 1 0 0 3 1.98 33687 1 1 0 3 1.92
16 0 0 0 4 2.0 764405 1 1 1 1 4 2.07
17 1 0 0 5 2.02 400801 0 0 0 0 5 1.99
18 0 0 0 6 # / 0! 562167 1 1 0 6 1.90
19 1 0 0 7 # / 0! 471789 1 1 1 7 1.85
Before reshuffling 500 cells: unsatisfactory
After rearranging 500 cells: normal
Conclusion: a smart fake is revealed, because it is not programmed
all possible options and skew due to synthesis algorithm .
A fake shuffled sequence turns into a random sequence.
Conclusion: realistically identify fake sequences .
Software emulation I t op PRNG Micro S oft
program calculates pseudo-random sequences without using RND function.
'rnd ms .bas qbasic
OPEN "rndxxx.txt" FOR OUTPUT AS # 1
FOR i = 1 TO 55555: r = Rand
IF r <0.5 THEN PRINT # 1, 0 ELSE PRINT # 1, 1
'IF r <= 0.5 THEN PRINT # 1, 0 ELSE PRINT # 1, 1
'IF r <= 0.7 THEN PRINT # 1, 0 ELSE PRINT # 1, 1
NEXT: CLOSE
FUNCTION Rand: STATIC Seed
x1 = (Seed * 214013 + 2531011) MOD 2 ^ 24
Seed = x1: Rand = x1 / 2 ^ 24
END FUNCTION
Simplified C # implementation
for insertion into online compiler https://rextester.com/WXH62544
using System; // rndms.cs
namespace rndxx {public class Program
{public static void Main (string [] args)
{Random rand = new Random ();
for (int i = 1; i <5555; i ++)
{var d = rand.Next (2);
if (d <0.5)
Console.WriteLine ("0");
else Console.WriteLine ("1");
}}}}
Result: an accident of low power, supposedly understood by people as an accident supposedly normal.
General conclusions: true randomness is unnatural for people and it is possible to synthesize low-power or false sequences that are accepted by people and computers as random sequences .
Any sequence actually synthesized in programming languages and in tables ah Excel compatible.
challenge to overcome, I randomness solved recog and eat chance of normal or false in Excel spreadsheet with charts .
Which was required to prove.
natural randomness: main spectrum of repetitions
binary attribute exceeds theoretical values
1/4 = 25% of number of attributes or characters
quality accident: fill in all spectra
binary attribute according to theoretical values
natural chance: created by living creatures
or natural phenomena felt by living beings
funny: they don't show up anywhere
pseudorandom sequences that have passed diehard tests
and as if they didn't specifically translate diehard programs to excel & c#
examples of fraud using random sites
1. program outputs an even or odd number
lots of people have to guess parity.
students write a pseudo algorithm in your native language
where program examines data entered by people
and from site random reads data until
until he gets right number to win over people
be sure to prove getting a number from random site
goal: to warn your friends against gambling
2. program plays against people and synthesizes chains
numbers from random's website that are opposed to people's systems
for example, chains of only even 10 or alternating 12.
students write a pseudo algorithm in your native language
where program requests random site multiple times
be sure to prove getting a number from random site
for sake of proof of randomness and getting a chain of numbers
encrypts and informs player up to predictions in reality
containing a programmed override of player's system
goal: to warn your friends against gambling
Тасовка
тасуем и следим чтоб номер своё место не занял
пока без контроля стал ли массив биномиально лучше
создаём массив номеров подряд
и за 1 проход переставляем номер порядковый и случайный номер
и если номера переставляемых совпадают: крутящаяся строка мой почерк
проверяем массив и если есть номера на своих местах:
считаем количество и пишем массив как бракованный
помечая совпавшие знаком минус
на экран выводятся первые и крайние номера зато в файл возможно писать всё
как копировать текстовые результаты из окна неизвестно поэтому:
картинка показывает: 9 номеров качественно перетасовали с 6-й попытки
за 0 секунд
далее планирую вычислить стала ли последовательность истинно случайной
и видимо придётся перейти на индексы индексов как ячейки excel
вариант: тасовать чтоб каждый элемент переместился дальше 10% от места
ведь длинные массивы наверняка окажутся без повторов
результат видимый если сохранять на диск или рам диск
между ячейками минимум 10%
и количество повторных перетасовок: до 25% длины массива
контроль результата: открыть в блокноте и поиск 1.0
как отношение менее 10% и искомое отсутствует
значит тасуются элементы на расстоянии друг от друга минимум 10% массива
двоичные возникают если выявить чётность и нечётность
и сравнивая относительного среднего: меньше или больше
a = 100: DIM d(a): x=0: k=0: t$=CHR$(9): RANDOMIZE TIMER 'tas_ten.bas
PRINT ,: FOR i = 1 TO a: d(i)=i: NEXT
FOR i = 1 TO 5: PRINT d(i);: NEXT: PRINT ,
FOR i = a-3 TO a: PRINT d(i);: NEXT: z = TIMER
OPEN "b:/control.txt" FOR OUTPUT AS #1 ' ram disk
WHILE x < 1
v = 0: FOR i = 1 TO a
1 m = INT(RND*a)+1: IF ABS(d(i)-d(m)) < .1*a THEN v = v+1: GOTO 1
PRINT #1, ABS(d(i)-d(m)); t$; d(i); t$; d(m); t$; i; t$; m; t$; d(i)/d(m); t$; d(m)/d(i)
t = d(i): d(i) = d(m): d(m) = t
NEXT
s = 0: FOR i = 1 TO a
IF d(i) = i THEN s = s+1
NEXT
5 k = k+1: PRINT: PRINT s; v,: IF s=0 THEN x = x+1
FOR i = 1 TO 5
IF d(i) = i THEN PRINT -d(i); ELSE PRINT d(i);
NEXT: PRINT ,
FOR i = a-3 TO a
IF d(i) = i THEN PRINT -d(i); ELSE PRINT d(i);
NEXT
WEND: PRINT: PRINT " = "; k, TIMER-z: END
ABS d(i) d(m) i m d(i)/d(m) d(m)/d(i)
41 70 29 91 18 2.413793 0.4142857
59 24 83 92 38 0.2891566 3.458333
14 32 46 93 44 0.6956522 1.4375
23 10 33 94 88 0.3030303 3.3
29 19 48 95 36 0.3958333 2.526316
11 41 30 96 11 1.366667 0.7317073
38 1 39 97 21 2.564103E-02 39
60 26 86 98 55 0.3023256 3.307692
17 4 21 99 58 0.1904762 5.25
26 100 74 100 59 1.351351 0.74
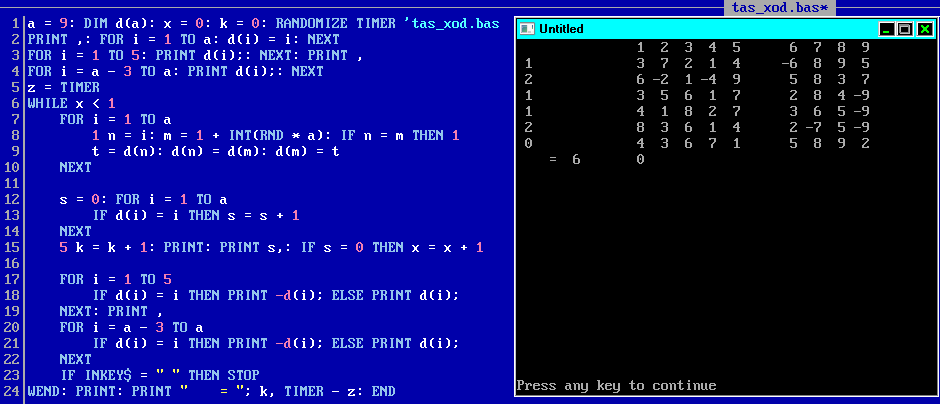
Думаю данная моя давнишняя разработка
поможет синтезировать качественные случайные
Shuffle
shuffle and make sure that number does not take its place
so far without control has array become binomially better
we create an array of numbers in a row
and in 1 pass we rearrange serial number and a random number
and if numbers of rearranged ones match: spinning line is my handwriting
check array and if there are numbers in their places:
we count number and write array as defective
marking matched ones with a minus sign
first and last numbers are displayed on screen but it is possible to write everything to file
how to copy text results from window is unknown therefore:
picture shows: 9 numbers were qualitatively shuffled from 6th attempt
in 0 seconds
next I plan to calculate whether sequence has become truly random
and apparently I will have to switch to index indexes as excel cells
option: shuffle so that each element moves further than 10% of place
because long arrays will certainly be without repetitions
result is visible if saved to disk or ram disk
between cells at least 10%
and number of repeated shuffles: up to 25% of array length
result control: open in notepad and search 1.0
as ratio is less than 10% and desired is missing
this means that elements are shuffled at a distance of at least 10% of array from each other
binary arise if you identify parity and odd
and comparing relative average: less or more
Исследование и преобразование сортировкой псевдослучайных последовательностей
ai-news.ru/2020/02/issledovanie_i_preobrazovanie_sortirovkoj_psevdosluchajnyh_posledovatelnost.html
Research and sorting transformation pseudo random sequences priority of russia
dev.to/andreydanilin/research-and-sorting-transformation-pseudo-random-sequences-priority-of-russia-37ah
Фальсификация случайности и преобразование сортировкой псевдослучайных последовательностей
ai-news.ru/2020/02/falsifikaciya_sluchajnosti_i_i_preobrazovanie_sortirovkoj_psevdosluchajnyh.html
Falsification of randomness and transformation by sorting of pseudorandom sequences priority of russia
dev.to/andreydanilin/falsification-of-randomness-and-transformation-by-sorting-of-pseudorandom-sequences-priority-of-russia-30fi
kenokeno.ucoz.ru/fips/2020611555.htm
|