Принцип 80/20 % и биномиальность 

Почему явления разделяются по принципу 80/20 % и подобным принципам? 

Явления разделяются по мощности биномиально, 
где каждое явление в 2 раза больше ближайшего по мощности явления 

Численно формируется ряд x+0,5x+0,25x+0,125x = 100
и значения группируются по мощности (x+0,5x)+(0,25x+0,125x) = 100

Решая в десятичных числах без дробей, получаем x=100/1,875 и x=53,33

Тогда 0,5x=26,67 и 0,25x=13,33 и 0,125x=6,67

Возвращаясь в интеграл суммы мощности явлений, получаем: 
53,33 +26,67 = 80 и 13,33 +6,67 = 20 в сумме 100% = 80% + 20%
или 
53,33 +6,67 = 60 и 26,67 +13,33 = 40 в сумме 100% = 60% + 40%

Обратная задача, начиная с наименьшего по мощности явления 
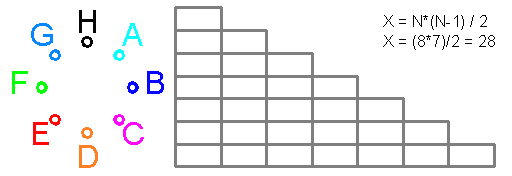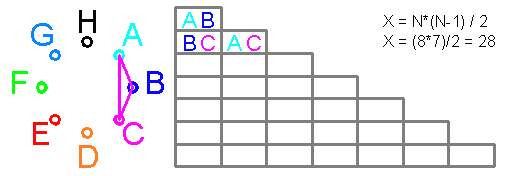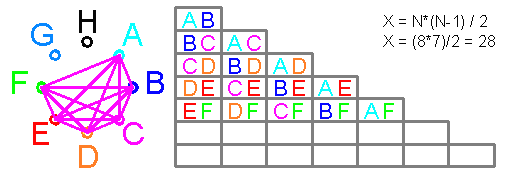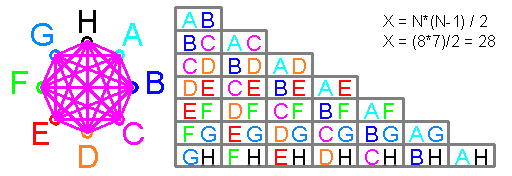
из уравнения x+2x+4x+8x=100 получаем x =100/15 =6,67

Проверяя все варианты через дроби натуральные и десятичные, 
решение показывает разделение 80% и 20% расчётное точное  

1 / 15 = около 6% 
3 / 15 = 20% точно 
5 / 15 = 1/3 треть точно или около 33% 
6 / 15 = 40% точно или 2 / 5 
9 / 15 = 60% точно или 3 / 5 
10 / 15 = 2/3 точно или около 66% 
12 / 15 = 80% точно 

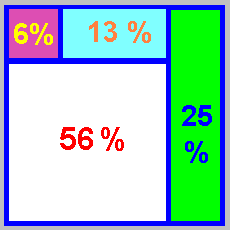
Квадрат 10x10 =100 делится в точке 2x3 клетки, 
ограничивая области 2x3=6 и 2x7=14 и 3x8=24 и 7x8=56 

Округляя =6% +14% +24% +56%, получаются суммы 
=6% +14% = 20% и =24% +56% = 80% 
и =6% +24% = 30% и =14% +56% = 70% 

Выявив 80% выгодных товаров и исключив 20% мало выгодных, 
среди оставшихся товаров вновь возникнет
фрактальное расслоение на 80% и на 20% 

Население активные 20% включают: 6% активнейшие и 14% менее активных
и так же пассивные 80% включает: 56% обыватели и 24% равнодушные 

Квадрат 4х4=16 просто делить на четверти 
1 / 16 = 6%
2 / 16 = 13%
4 / 16 = 25% точно  
9 / 16 = 56% 
12 / 16 = 75% точно = (1+2+9) / 16 

Выражая через кратные 5:
55% +25% +15% +5% = 100%

Представив явления визуально, как ряд элементов, 
размер каждого элемента зависит от порядкового места 

Допустим, биномиальный множитель M = 1/2 = 0,5, 
тогда зависимый от размера E(0) элемента 0-го
размер E(N) элемента с номером N равен E(N) = E(0) * M^N 

Проверка: E(0)=53,33 и N=3, тогда E(3) = 53,33 *0,5^3 = 6,67

Номер элемента N вычисляет обратная задача: 
в какую степень возвести множитель для получения результата 
M^N = E(n)/E(0) и N = log(E(n)/E(0); M)

Проверка: N = log(6,67/53,33; 0,5) = 3

Возможна троичность и разделение тернарное 
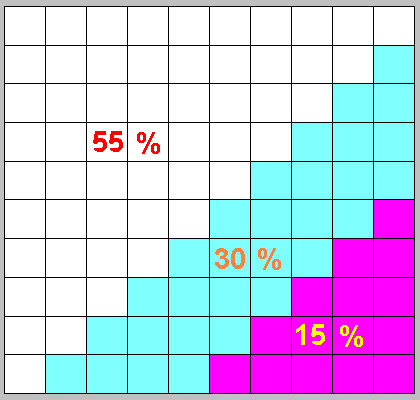
=15% +30% +55% = 100%

Итого: выражение вида "20% действий создают 80% результатов" 
интегрально складывается из 2-х независимых явлений, 
каждое из которых распределяется биномиально 

Принцип 80/20 % обычно называют "принцип Парето" 

Биномиальность создаётся как 100% делить на 15 
где 15 вычисляется из уравнения x+2x+4x+8x=100 
и где x =100/15 =6,67 и проверяя все множители 
получаются дроби натуральные и десятичные 
и показывает разделение 80% и 20% расчётное и точнее 
1 из 15 = 6% и 3 из 15 = 20% и 5 из 15 = 33% треть 
и 6 из 15 = 40% как 2 из 5 и 9 из 15 = 60% как 3 из 5 
и 10 из 15 = 2 трети 66% и 12 из 15 = 80% 
или округляя =6% +14% +24% +56% 
получаются суммы =6% +14% = 20% и =24% +56% = 80% 
и =6% +24% = 30% и =14% +56% = 70% 
и получается троичность =15% +30% +55% = 100%

В жизни таблица 2х2=4 возникает очень часто
например 2 варианта
быстро медленно и дёшево дорого
создают 4 комбинации

медленно дорого
медленно дёшево
быстро дорого
быстро дёшево

Поэтому 4 компонента достаточно

Энциклопедия

Биномиальность - это свойство или характеристика, 
относящаяся к биномам или биномиальным выражениям. 

Биномиальное выражение представляет собой алгебраическое выражение, 
состоящее из 2-х членов, разделенных знаком операции сложения или вычитания. 

Примером может служить выражение (a + b), где a и b - это переменные, 
а знак + обозначает операцию сложения. 

Биномиальные выражения могут быть использованы в алгебре, комбинаторике, 
теории вероятностей и других областях математики.

В более широком смысле, биномиальность также может относиться 
к биномиальным коэффициентам, которые являются числовыми коэффициентами, 
связанными с разложением биномиального выражения по формуле Бинома Ньютона. 

Биномиальные коэффициенты широко используются в комбинаторике 
и теории вероятностей для подсчета количества вариантов или комбинаций. 

Принцип 80/20 % обычно называют принцип Парето 
 

Principle 80/20 % and binomiality

Why are phenomena divided according to 80/20% principle and similar principles?

Phenomena are divided by power binomially,
where each phenomenon is 2 times larger than nearest phenomenon in power

Series x+0.5x+0.25x+0.125x = 100 is numerically formed
and values are grouped by power (x+0.5x)+(0.25x+0.125x) = 100

Solving in decimal numbers without fractions we get x=100/1.875 and x=53.33

Then 0.5x=26.67 and 0.25x=13.33 and 0.125x=6.67

Returning to integral of sum of power of phenomena, we get:
53.33+26.67 = 80 and 13.33+6.67 = 20 in sum of 100% = 80% + 20%
or
53.33+6.67 = 60 and 26.67+13.33 = 40 in sum of 100% = 60% + 40%

Inverse problem, starting with smallest power phenomenon
from equation x+2x+4x+8x=100, we get x =100/15 =6.67

Checking all options through natural and decimal fractions,
solution shows separation of 80% and 20% calculated exact

1 / 15 = about 6%
3 / 15 = 20% accurate
5 / 15 = 1/3 third exactly or about 33%
6 / 15 = 40% accurate or 2/5
9 / 15 = 60% accurate or 3/5
10 / 15 = 2/3 exactly or about 66%
12 / 15 = 80% accurate

Square 10x10 =100 is divided at point 2x3 cells
bounding areas 2x3=6 and 2x7=14 and 3x8=24 and 7x8=56

Rounding up =6% +14% +24% +56% amounts are obtained
=6% +14% = 20% and =24% +56% = 80%
and =6% +24% = 30% and =14% +56% = 70%

Having identified 80% of profitable goods and excluded 20% of little profitable
among remaining goods, fractal stratification by 80% and by 20%

Active 20% population includes 6% of most active and 14% of less active
and also passive 80% includes 56% of inhabitants and 24% of indifferent

Square 4x4=16 is simply divided into quarters
1 / 16 = 6%
2 / 16 = 13%
4 / 16 = 25% accurate
9 / 16 = 56%
12 / 16 = 75% accurate = (1+2+9) / 16

Expressing by multiples 5:
55% +25% +15% +5% = 100%

Presenting phenomena visually as a series of elements,
size of each element depends on ordinal location

Let's say binomial multiplier M = 1/2 = 0.5,
then size of E(0) element of 0th dependent on
size of E(N) element with number N is equal to E(N) = E(0) * M^N

Check: E(0)=53.33 and N=3, then E(3) = 53.33*0.5^3 = 6.67

Number of element N is calculated by inverse problem:
to what extent should multiplier be raised to get result
M^N = E(n)/E(0) and N = log(E(n)/E(0); M)

Check: N = log(6.67/53.33; 0.5) = 3

Trinity and ternary division are possible
=15% +30% +55% = 100%

Total: an expression of form "20% of actions create 80% of results"
integrally consists of 2 independent phenomena,
each of which is distributed binomially

80/20% principle is commonly referred to as "Pareto principle"

Binomiality is created as 100% divided by 15
where 15 is calculated from equation x+2x+4x+8x=100
& where x =100/15 =6.67 & checking all factors
get natural & decimal fractions
& shows separation of 80% & 20% calculated & more precisely
1 from 15 = 6% & 3 from 15 = 20% & 5 from 15 = 33% third
& 6 from 15 = 40% as 2 from 5 & 9 from 15 = 60% as 3 from 5
& 10 from 15 = 2 thirds 66% & 12 from 15 = 80%
or rounding =6% +14% +24% +56%
resulting amounts are =6% +14% = 20% & =24% +56% = 80%
& =6% +24% = 30% & =14% +56% = 70%
& result is a trinity = 15% + 30% + 55% = 100%

In life table 2x2=4 appears very often

For example 2 options
fast slow and cheap expensive
create 4 combinations

slow expensive
slow cheap
fast expensive
fast cheap

Therefore 4 components are enough

Encyclopedia

Binomiality is a property or characteristic
related to binomials or binomial expressions.

A binomial expression is an algebraic expression
consisting of 2 terms separated by sign of an addition or subtraction operation.

An example is expression (a + b), where a and b are variables,
and + sign denotes addition operation.

Binomial expressions can be used in algebra, combinatorics,
probability theory and other areas of mathematics.

More broadly, binomiality can also refer to
to binomial coefficients, which are numerical coefficients
associated with decomposition of a binomial expression by Newton Binomial formula.

Binomial coefficients are widely used in combinatorics
and probability theory to count number of variants or combinations.