Деление подобных случаев подряд
ДПСП = деление подобных случаев подряд
олицетворяет вероятность вероятности
DSCR = division of similar cases in a row
personifies probability of probability
ANZR = Abteilungnicht Zufall in der Reihe
personifiziert die Wahrscheinlichkeit der Wahrscheinlichkeit
DCSS = division de cas similaires a la suite
en ligne personnifie la probabilite de probabilite
ДПСП = деление подобных случаев подряд
Математические законы справедливы во всех лотереях и
важно знать дюжину пределов подобных случаев подряд наизусть.
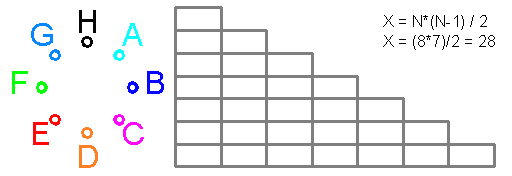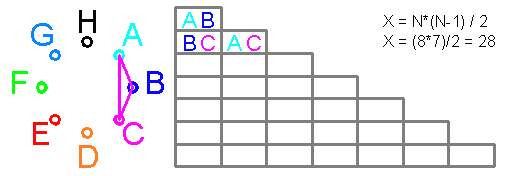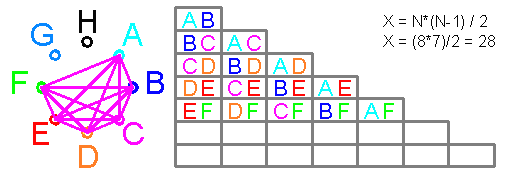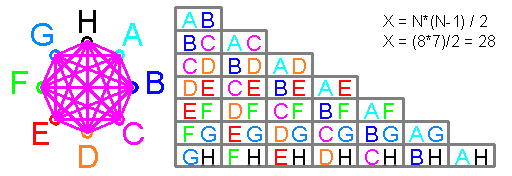
Умножение постоянных вероятностей C+р^N=1
олицетворяет вероятность вероятности и создаёт формулу
N = LOG(1-C)/LOG(1-p)
С - вероятность выигрыша гарантированного
р - вероятность выигрыша события.
Например задача: число подобных случаев подряд
с вероятностью 99% для вероятности 48,65%
N = LOG(1-0,99)/LOG(1-0,4865) = 7
и значит на вероятности около 50%
легко неугадать 7 раз подряд
Упрощённо можно рассчитывать по формуле N = 7+(5*(1/x-2))
например х=0,1 N= 47 нормально и х=0,78 N= 4 нормально.
Те же формулы справедливы и для вероятностей выше 50%.
Геометрические прогрессии содержащие в условии или в решении
смысл "в какую степень надо возвести" решаются через логарифм.
Используя предел подобных случаев подряд в таблицах
обнаруживается волна или период угадываний 2-х видов:
1-й вид: волна или период - как сама вероятность
через количество тиражей и там где вероятность 1/3
там волна или период угадывания через 3 тиража;
2-й вид: волна или период - как предел подобных случаев подряд
и там где вероятность 1/3 там волна или период угадывания
через 12 тиражей и возможно несколько ставок при сигнале.
Нобелевская премия сама себя не получит
Nobel Prize will not receive itself
Nobelpreis wird sich nicht erhalten
Le prix Nobel ne se recevra pas
Il Premio Nobel non ricevera se stesso
Успех
Вероятность |
1 из ...
|
|
2 |
3 |
4 |
5 |
10 |
100 |
1,5 |
1,33 |
|
1 /… |
Win 1 from…
Probability |
|
Отказ
Вероятность
|
% |
|
50% |
67% |
75% |
80% |
90% |
99% |
33% |
25% |
|
% |
Lose %
Probability |
| |
|
|
Подобные ПОДРЯД |
|
|
|
| Надёжность |
90 % |
|
3 |
6 |
8 |
10 |
22 |
230 |
2 |
1 |
|
90 |
Reliability |
| Надёжность |
99 % |
|
7 |
12 |
16 |
21 |
44 |
458 |
4 |
3 |
|
99 |
Reliability |
| Надёжность |
99,5 % |
|
10 |
17 |
24 |
31 |
66 |
687 |
6 |
4 |
|
99,9 |
Reliability |
| Надёжность |
50 % |
|
1 |
2 |
2 |
3 |
7 |
69 |
1 |
0 |
|
50 |
Reliability |
| Надёжность |
95 % |
|
4 |
7 |
10 |
13 |
28 |
298 |
3 |
2 |
|
95 |
Reliability |
| |
|
|
Similar IN ROW |
|
|
|
Успех
Вероятность |
1 из ...
|
|
2 |
3 |
4 |
5 |
10 |
100 |
1,5 |
1,33 |
|
1 /… |
Win 1 from…
Probability |
Отказ
Вероятность |
% |
|
50% |
67% |
75% |
80% |
90% |
99% |
33% |
25% |
|
% |
Lose %
Probability |
Угадать вероятность 25%=1/4=0,25 и получить надёжность 99% нужно 16 подряд действий
Волны вероятности повышают надёжность
Теория и Практика 0 и 1
* Теория из моих тем АнтиИгроМаниЯ *
Математические законы справедливы во всех вероятностях и
важно знать дюжину пределов подобных подряд наизусть.
Умножение постоянных вероятностей C+р^N=1
олицетворяет вероятность вероятности и создаёт формулу
N = LOG(1-C)/LOG(1-p)
С - вероятность выигрыша гарантированного
р - вероятность выигрыша события.
Например: с вероятностью 99% для вероятности 48,65%
число подобных случаев подряд N = LOG(1-0,99)/LOG(1-0,4865) = 7
и значит на вероятности около 50% легко неугадать 7 раз подряд
Упрощённо возможно рассчитывать по формуле N = 7+(5*(1/x-2))
например х=0,1 N= 47 нормально и х=0,78 N= 4 нормально.
Те же формулы справедливы и для вероятностей выше 50%.
Геометрические прогрессии содержащие в условии или в решении
смысл "в какую степень надо возвести" решаются через логарифм.
* Начало *
Используя предел подобных случаев подряд в таблицах
обнаруживается волна или период угадываний 2-х видов:
1-й вид: волна или период - как сама вероятность
через количество тиражей и там где вероятность 1/3
там волна или период угадывания через 3 тиража;
2-й вид: волна или период - как предел подобных случаев подряд
и там где вероятность 1/3 там волна или период угадывания
через 12 тиражей и возможно несколько ставок при сигнале
* Ставки *
Виртуально повышаем ставки при проигрыше
и понижаем ставки при выигрыше до минимальной ставки
Реально ставим только соблюдая Квадрат Экономии Данилиных
* Практика *
Синтезируем 50 номеров 0 и 1 контролируя сумму 25
=случмежду(0;1)
случ: 00111000000011111101010011111000001010111010000111
специально назначены 7 подряд проигрышей 0000000
получаем 4 результата вида:
предполагали выигрыш/проигрыш и угадали/неугадали:
А - угадан выигрыш - 1-1 - участие и выигрыш
Б - угадан проигрыш - 0-0 - неучастие
В - неугадан выигрыш - 0-1 - неучастие
Г - неугадан проигрыш - 1-0 - участие и проигрыш
* Практика: 001 *
идея: пропущены несколько бывших бы проигрышными
и пропущен единственный бывший бы выигрышным
обозначения: "!" = сигнал и "." = ожидание
случ: 00111000000011111101010011111000001010111010000111
коды: ..!А........!А..........!А........!Г...........!А.
обособим коды А&Г = АААГА = выигрышно: А > Г
без повышения ставок и возможны 2 ставки подряд
после сигнала и проигрыша и остановка при выигрыше
* Практика: 1-я волна *
сопоставим с идеальным распределением
идея: 01010101010101010101010101010101010101010101010101
случ: 00111000000011111101010011111000001010111010000111
коды: БГВАВГБГБГБГВАВАВАБАБАБГВАВАВГБГБГВГВГВАВГВГБГБАВА
обособим коды А&Г = ГАГГГГАААААГААГГГГГАГГГАА
видим 5 проигрышей подряд и баланс цел
т.к. по простейшей системе у-2-ения ставок при проигрыше
требуется 7 проигрышей подряд до обнуления баланса
начав с минимальной ставки 1%: = 2^7 = 128 процентов баланса
идеи сплошь одинаковых признаков будут повторять
картину совпадений с тем же числом подобных случаев подряд
идея: 00110011001100110011001100110011001100110011001101
случ: 00111000000011111101010011111000001010111010000111
коды: ББААВБГГББГГВВААВВГАБВГГВВААВБГГББАГВБААВБАГББГАВА
обособим коды А&Г = ААГГГГААГАГГААГГАГАААГГАА
видим 5 подряд проигрышей и баланс цел
* Практика: 2-я волна *
обозначения: "!" = сигнал и "." = ожидание
идея: пропускаем 7 подряд как 0000000
и ставим максимум 2-жды подряд или до выигрыша
случ: 00111000000011111101010011111000001010111010000111
коды: ...........!А.....................................
в примере мог быть проигрыш и видим 1 выигрыш редкий
поэтому важно следить за всеми признаками
идея: упрощённо пропускаем 4 подряд как 0000
и ставим максимум 2-жды подряд или до выигрыша
та же формула включающая логарифм и надёжность ниже
случ: 00111000000011111101010011111000001010111010000111
коды: ........!ГГ.....................!ГА...........!А..
обособим коды А&Г = ГГГАА
видим 3 подряд проигрышей и баланс цел
зато пропуская 3 подряд как 000 было бы рискованнее
* Практика: 2-ые волны *
совпадения на 2-й волне от предыдущего совпадения
прибавляем шаг как расчётный предел подобных случаев подряд
обозначения: "!" = сигнал и "." = ожидание
случ: 00111000000011111101010011111000001010111010000111
коды: ...123456!Г......123456!А...123456!Г..............
коды: ....123456!Г......123456!А...123456!А.............
коды: .....123456!А.......123456!А.......123456!А.......
коды: .............123456!Г.123456!Г.......123456!Г.....
коды: ..............123456!А...123456!Г......123456!Г...
коды: ...............123456!Г...123456!Г......123456!А..
коды: ................123456!Г...123456!А......123456!А.
обособим коды А&Г = ГГАГАГГАААГГГАГААГГАА
видим 3 подряд проигрышей и баланс цел
* Практика: 2 волны и больше волн *
идея 001: пропущены несколько бывших бы проигрышными
и пропущен единственный бывший бы выигрышным
обозначения: "!" = сигнал и "." = ожидание
случ1: 00111000000011111101010011111000001010111010000111
коды1: ..!А........!А..........!А........!Г...........!А.
случ2: 11100001011101010000011111001010111111000000011100
коды2: .......!Г...........!A......!Г...............!А...
где случ2 обратная последовательность от случ1 для эксперимента
обособим коды А&Г = АГАААГГАА = выигрышно: А > Г
без повышения ставок и возможны 2 ставки подряд
после сигнала и проигрыша и остановка при выигрыше
видим 2 подряд проигрыша и баланс цел
предположим сложились ситуации независимые все возможные:
случ3: 0001000010000110000011
коды3: ...!Г...!Г...!А.....!A
случ4: 0001000011000100000011
коды4: ...!Г...!A...!Г.....!А
одновременно: ГГ / ГА / АГ / АА
значит были: 1 выигрыш и 1 проигрыш и 2 возврата
вероятность выигрыша 1/4 = 25 %
вероятность проигрыша 1/4 = 25 %
вероятность возврата 1/2 = 50 %
всё с целью: деление подобных случаев подряд
и тоже то же для 3-х и более независимых признаков
и для идей про шаг свыше предела подобных случаев подряд
* Вывод *
Волны вероятности повышают надёжность
Нобелевская премия сама себя не получит
Nobel Prize will not receive itself
Nobelpreis wird sich nicht erhalten
Le prix Nobel ne se recevra pas
Il Premio Nobel non ricevera se stesso
логарифмы недоступны массово
из-за воображаемой сложности
все знают: = 5+5+5 = 15
значит на сколько нужно разделить 15
чтобы получить 5: ответ = 15/5 = 3
однако такой же принцип = 5*5*5 = 125
и вопрос в какую степень возвести 5
чтобы получить 125 ставит в тупик
и народ избегает якобы сложной задачи
решаемой через логарифм =log(125;5)
= 3 значит надо возвести 5 в 3-ю степень
применение данной задачи к величинам 0<1
решает задачи вероятности и надёжности

DNCR = division not coincidence in row
Mathematical laws are valid in all lotteries and
It is important to know a dozen limits of similar cases in a row by heart.
Multiplication of constant probabilities C + p ^ N = 1
personifies probability of probability and gives formula
N = LOG (1-C) / LOG (1-p)
C is probability of winning guaranteed
p is probability of winning an event.
For example, problem: number of similar cases in a row
with a probability of 99% for probability of 48.65%
N = LOG (1-0.99) / LOG (1-0.4865) = 7
and therefore probability of about 50%
easy to guess 7 times in a row
Simplified can be calculated by formula N = 7+ (5 * (1 / x-2))
for example, x = 0.1 N = 47 is normal and x = 0.78 N = 4 is normal.
same formulas are valid for probabilities above 50%.
geometric progressions containing in condition or in solution
meaning "to what extent it is necessary to erect" is solved through logarithm.
using discrepancy limit in a row in tables
there is a wave or a guessing period of 2 kinds:
1st kind: wave or period - like probability itself
through number of runs and there where probability of 1/3
there is a wave or a guessing period in 3 draws;
2nd type: wave or period - as limit of inconsistencies in a row
and where probability of 1/3 there is a wave or guessing period
through 12 runs and maybe several bets on signal.
Nobel Prize will not receive itself
ANZR = Abteilungnicht Zufall in der Reihe
Mathematische Gesetze sind in allen Lotterien gültig und
Es ist wichtig, ein Dutzend Unstimmigkeitsgrenzen hintereinander auswendig zu kennen.
Multiplikation konstanter Wahrscheinlichkeiten C + p ^ N = 1
personifiziert die Wahrscheinlichkeit der Wahrscheinlichkeit und ergibt die Formel
N = LOG (1-C) / LOG (1-p)
C ist die Gewinnwahrscheinlichkeit garantiert
p ist die Wahrscheinlichkeit, ein Ereignis zu gewinnen.
Zum Beispiel das Problem: die Anzahl der Nichtübereinstimmungen in einer Zeile
mit einer Wahrscheinlichkeit von 99% für die Wahrscheinlichkeit von 48,65%
N = LOG (1-0,99) / LOG (1-0,4865) = 7
und daher die Wahrscheinlichkeit von etwa 50%
leicht zu erraten 7 mal hintereinander
Vereinfacht kann mit der Formel N = 7+ (5 * (1 / x-2)) berechnet werden
zum Beispiel ist x = 0,1 N = 47 ist normal und x = 0,78 N = 4 ist normal.
Die gleichen Formeln gelten für Wahrscheinlichkeiten über 50%.
Nobelpreis wird sich nicht erhalten
DPCL = division pas la coincidence en ligne
Les lois mathématiques sont valables dans toutes les loteries et
Il est important de connaître une douzaine de limites de désaccord dans une rangée par coeur.
La multiplication des probabilités constantes C + p ^ N = 1
en ligne personnifie la probabilite de probabilite et donne la formule
N = LOG (1-C) / LOG (1-p)
C est la probabilité de gagner garanti
p est la probabilité de gagner un événement.
Par exemple, le problème: le nombre de discordances dans une rangée
avec une probabilité de 99% pour la probabilité de 48,65%
N = LOG (1-0.99) / LOG (1-0.4865) = 7
et donc la probabilité d'environ 50%
facile à deviner 7 fois de suite
Simplifié peut être calculé par la formule N = 7+ (5 * (1 / x-2))
par exemple, x = 0,1 N = 47 est normal et x = 0,78 N = 4 est normal.
Les mêmes formules sont valables pour les probabilités supérieures à 50%.
Le prix Nobel ne se recevra pas
Успех
Вероятность |
1 из ...
|
|
2 |
3 |
4 |
5 |
10 |
100 |
1,5 |
1,33 |
|
1 /… |
Win 1 from…
Probability |
Отказ
Вероятность |
% |
|
50% |
67% |
75% |
80% |
90% |
99% |
33% |
25% |
|
% |
Lose %
Probability |
| |
|
|
Подобные ПОДРЯД |
|
|
|
| Надёжность |
90 % |
|
3 |
6 |
8 |
10 |
22 |
230 |
2 |
1 |
|
90 |
Reliability |
| Надёжность |
99 % |
|
7 |
12 |
16 |
21 |
44 |
458 |
4 |
3 |
|
99 |
Reliability |
| Надёжность |
99,5 % |
|
10 |
17 |
24 |
31 |
66 |
687 |
6 |
4 |
|
99,9 |
Reliability |
| Надёжность |
50 % |
|
1 |
2 |
2 |
3 |
7 |
69 |
1 |
0 |
|
50 |
Reliability |
| Надёжность |
95 % |
|
4 |
7 |
10 |
13 |
28 |
298 |
3 |
2 |
|
95 |
Reliability |
| |
|
|
Similar IN ROW |
|
|
|
Успех
Вероятность |
1 из ...
|
|
2 |
3 |
4 |
5 |
10 |
100 |
1,5 |
1,33 |
|
1 /… |
Win 1 from…
Probability |
Отказ
Вероятность |
% |
|
50% |
67% |
75% |
80% |
90% |
99% |
33% |
25% |
|
% |
Lose %
Probability |
Guessing for probability of 25%=1/4=0.25 and getting 99% reliability requires 16 actions in a row

деление подобных случаев подряд создаёт парадокс:
теоретическая вероятность совпадения
и меньшее число подобных случаев подряд
неизвестно: ? повысилась ли вероятность угадать ?
например: допустим теоретическое подобных случаев подряд 7
и проведя массу опытов видим вплоть до 12 подобных случаев
однако применив другие признаки видим в массе опытов
только максимум 5 подобных случаев подряд и неясно улучшили ли
division of similar cases in a row creates a paradox:
theoretical probability of coincidence
and a smaller number of similar cases in succession
unknown:? Has probability of guessing increased?
for example: assume a theoretical similar cases in succession 7
and after conducting a lot of experiments we see up to 12 discrepancies
However by applying other features we see in mass of experiments
Only a maximum of 5 similar cases in a row and it is unclear whether
la division des discordances dans une rangee crуee un paradoxe:
probabilite theorique de coincidence
et un plus petit nombre de disparites successives
inconnu :? La probabilite de deviner a-t-elle augmente?
par exemple: supposons une inadequation theorique successive 7
et apres avoir mene beaucoup d'experiences nous voyons jusqu'a 12 divergences
Cependant en appliquant d'autres fonctionnalites que nous voyons dans la masse d'experiences
Seulement un maximum de 5 discordances dans une rangee et il n'est pas clair si
Die Aufspaltung von Fehlanpassungen in Folge schafft ein Paradox:
theoretische Wahrscheinlichkeit der Ubereinstimmung
und eine kleinere Anzahl von Fehlanpassungen in Folge
unbekannt :? Hat sich die Wahrscheinlichkeit des Ratens erhoht?
Zum Beispiel: Nehmen Sie eine theoretische Diskrepanz in Folge an 7
und nachdem wir viele Experimente durchgefuhrt haben sehen wir bis zu 12 Diskrepanzen
Durch Anwendung anderer Merkmale sehen wir jedoch in der Masse der Experimente
Nur maximal 5 Fehlanpassungen hintereinander und es ist unklar ob
la divisione dei disallineamenti di fila crea un paradosso:
probabilita teorica di coincidenza
e un minor numero di disallineamenti in successione
sconosciuto: La probabilita di indovinare e aumentata?
per esempio: ipotizza una mancata corrispondenza teorica in successione 7
e dopo aver condotto un sacco di esperimenti vediamo fino a 12 discrepanze
Tuttavia applicando altre caratteristiche che vediamo nella massa di esperimenti
Solo un massimo di 5 disallineamenti di fila e non e chiaro se

про включение в азартные игры
гуманитарный пример: трамвай
трамваи ночью не ходят
трамваи начинают ходить утром
трамваи ходят днём
приезжий из гостиницы видит езду трамваев
и приезжий предполагает ехать максимально рано
выйдя на трамвай ночью
придётся ждать до утра и потерять время впустую
значит проиграл
выйдя на трамвай днём
возможно упустить предыдущие трамваи
поэтому ехать дольше
да и возможно опоздать на последний дневной трамвай
значит проиграл или не выиграл
думаю оптимально: пропустив ночь без трамваев
увидеть 1-й утренний трамвай и встретить следующий трамвай
думаю оптимально: пропустив не играя бывший бы проигрышным
непрерывный период азартной игры
увидеть сигнал игры как возможно начавшееся облако совпадений
и участвовать в ближайший системный случай
выключаясь из игры на периоды бывшие бы проигрышными
надеясь на деление подобных случаев подряд
математический форум обсуждая проверку последовательности
случайной на случайность показал: там математики только копируют
чужую демагогию из старых книг и даже не способны задуматься
над распределением повторений событий подряд
неудивительно: в учебниках теории вероятностей искомые формулы
случайно отсутствуют но могли бы смоделировать в excel
на примере вероятности 50% сколько раз было 7 раз подряд
и другие количества признаков подряд
чтоб соответствовали формулам включающим логарифм
иначе генератор случайных чисел ... фальшивый
Waves of probability increase reliability
Theory and Practice 0 and 1
* Theory of my Anti-Game-Mania Topics *
Mathematical laws are valid in all probabilities and it
is important to know a dozen of similar cases limits in a row.
Investigating logarithm is obtained:
formula including logarithm follows from calculation
probabilities of guessing consecutive events
For example, simplest: 0.7*0.7*0.7 = 0.7^3 = 0.343
degree to which it is necessary to build 0.7 to get 0.343
and in 20th century formula was restored by Andrey Danilin
N = LOG(0.343)/LOG(0.7) = 3
and corresponding formula for not guessing
Multiplication of constant probabilities C+p^N = 1
and in 20th century formula was restored by Andrey Danilin
N = LOG(1-C)/LOG(1-p)
C — probability of winning guaranteed
p — probability of winning event.
Example task: number of similar cases in a row
with a probability of 99% for a probability of 48.65%
and in 20th century formula was restored by Andrei Danilin
N = LOG(1-0,99)/LOG(1-0,4865) = 7
and that means about 50% probability
easy to guess 7 times in a row
Easily possible to count:
formula was discovered by Andrey Danilin N = 7+(5*(1/x-2))
and for example, x=0.1 N=47 is normal and x=0.78 N=4 is normal.
same formulas are valid for probabilities above 50%.
Geometric progression contained in condition or in solution
meaning of “degree to which it is necessary to build”
is solved through logarithm
* Start *
Using similar cases limit in a row in tables
a wave or a period of guessing of 2 types is detected:
1st type: wave or period — as probability itself
through number of runs and where probability is 1/3
there is a wave or guessing period after 3 runs;
2nd type: wave or period — as limit of discrepancies in a row
and where probability is 1/3 there is a wave or guessing period
in 12 draws and possibly several bets on signal
* Rates *
Virtually raise stakes when you lose
and lower stakes when winning to minimum bet
Really set only observing Quadrat Economy Danilins
* Practice *
We synthesize 50 numbers 0 and 1 controlling amount of 25
case: 00111000000011111101010011111000001010111010000111
specially assigned 7 consecutive losses 0000000
we get 4 results of form:
assumed a win / loss and guessed / failed to guess:
A — guess win — 1-1 — participation and win
E — guess loss — 0-0 — non-participation
I — not won — 0-1 — non-participation
U — loosing — 1-0 — participation and loss
* Practice: 001 *
idea: missing a few ex
and missed only former would be winning
notation: "!" = signal and "." = waiting
case: 00111000000011111101010011111000001010111010000111
code: ..!A........!A..........!A........!U...........!A.
isolate codes A&U = AAAUA = advantageous: A>U
no rate increase and 2 consecutive bids possible
after signal and loss and stop when winning
* Practice: 1st wave *
comparable to perfect distribution
idea: 01010101010101010101010101010101010101010101010101
case: 00111000000011111101010011111000001010111010000111
code: EUIAIUEUEUEUEAIAIAEAEAEUIAIAIUEUEUIUIUIAIUIUEUEAIA
isolate codes A&U = UUUUUAAAAAUAAUUUUUAUUUA
see 5 losses in a row and balance is intact
because according to simplest system of betting on losing
7 consecutive losses are required until balance is reset
starting with minimum rate of 1%: = 2^7 = 128 percent of balance
ideas are completely identical signs will repeat
picture of coincidence with same number of similar cases in a row
idea: 00110011001100110011001100110011001100110011001101
case: 00111000000011111101010011111000001010111010000111
code: EEAAIEUUEEUUIIAAIIUAEIUUIIAAIEUUEEAUIEAAIEAUEEUAIA
isolate codes A&U = AAUUUUAAUAUUAUAUUAUAAAUUAA
see 5 consecutive losses and balance is intact
* Practice: 2nd wave *
notation: "!" = signal and "." = waiting
idea: skip 7 consecutive as 0000000
and put a maximum of 2 in a row or before winning
case: 00111000000011111101010011111000001010111010000111
code: ...........!A.....................................
in example there could be a loss and see 1 win rare
therefore it is important to monitor all signs
Idea: simply skip 4 in a row like 0000
and put a maximum of 2 in a row or before winning
same formula including logarithm and reliability below
case: 00111000000011111101010011111000001010111010000111
code: ........!U......................!UA...........!A..
isolate codes A&U = UUAA
see 3 consecutive losses and balance is intact
but skipping 3 in a row as 000 would be more risk
* Practice: 2nd waves *
matches on 2nd wave from previous match
we add a step as a calculated limit of similar cases in a row
notation: "!" = signal and "." = waiting
case: 00111000000011111101010011111000001010111010000111
code: ...123456!U......123456!A...123456!U..............
code: ....123456!U......123456!A...123456!A.............
code: .....123456!A.......123456!A.......123456!A.......
code: .............123456!U.123456!U.......123456!U.....
code: ..............123456!A...123456!U......123456!U...
code: ...............123456!U...123456!U......123456!A..
code: ................123456!U...123456!A..... 123456!A.
isolate codes A&U = UUAUAUUAAAUUUAAUAUUAA
see 3 consecutive losses and balance is intact
* Practice: 2 waves and more waves *
idea 001: missing some ex would be losing
and missed only former would be winning
notation: "!" = signal and "." = waiting
case1: 00111000000011111101010011111000001010111010000111
code1: ..!U........!A..........!A........!U...........!A.
case2: 11100001011101010000011111001010111111000000011100
code2: .......!U...........!A......!U...............!A...
where case2 is reverse sequence from case1 for experiment
isolate codes A&U = UUAAAUUAA = advantageous: A>U
no rate increase and 2 consecutive bids possible
after signal and loss and stop when winning
see 2 consecutive losses and balance is intact
let us assume that all possible situations are independent:
case3: 0001000010000110000011
code3: ...!U...!U...!A.....!A
case4: 0001000011000100000011
code4: ...!U...!A...!U.....!A
at same time: UU / UA / AU / AA
so were: 1 win and 1 loss and 2 return
probability of winning 1/4 = 25 %
probability of losing 1/4 = 25 %
probability of return 1/2 = 50 %
everything with goal: division not coincidence in row
and also same for 3 or more independent signs
and for ideas about a step over limit of similar cases in a row
* Conclusion *
Waves of probability increase reliability
logarithms unavailable in bulk
because of imaginary complexity
everyone knows: = 5 + 5 + 5 = 15
it means by how much to divide 15
to get 5: answer = 15/5 = 3
however, same principle = 5 * 5 * 5 = 125
and question of what degree to build 5
to get 125 baffles
and people are avoiding supposedly difficult task
solved by logarithm =log(125;5)
= 3 means you need to build 5 to 3rd degree
application of this problem to values of 0 <1
solves problems of probability and reliability
about gambling
humanitarian example: tram
no trams at night
trams start walking in morning
trams go by day
visitor from hotel sees tram ride
and visitor intends to go as early as possible
getting off tram at night
will have to wait until morning and waste time
mean lost
getting on tram during day
it is possible to miss previous trams
so go longer
yes and maybe late for last day tram
then lost or not won
I think optimally: skipping night without trams
see 1st morning tram and meet next tram
I think optimally: skipping without playing former would be losing
continuous period of gambling
see signal of game as a possible cloud of coincidences
and participate in nearest system case
turning off from game for periods that would be losing
hoping to divide inconsistencies in a row
случайность натуральная: главный спектр повторов
двоичного признака превышает теоретические значения
1/4 = 25% количества признаков или символов
качественная случайность: заполняющая все спектры
двоичного признака согласно теоретическим значениям
натуральная случайность: созданная живыми существами
или природными явлениями ощущаемыми живыми существами
randomness natural: main spectrum of repetitions
binary attribute exceeds theoretical values
1/4 = 25% of number of attributes or characters
quality accident: fill in all spectra
binary attribute according to theoretical values
natural chance: created by living creatures
or natural phenomena felt by living beings
|